先備知識與注意事項
在經歷過Tree系列文章的洗禮後,接著要介紹的是Graph(圖)。
Graph比Tree更加廣義,其定義僅僅使用了集合(Set),並且不限制結構裡的node/vertex只能有唯一的parent field,因此,更多的問題能夠以Graph建立模型。
目錄
初探Graph的美妙:以課程與其先修科目為例
有一間大學的計算機科學學位之必修課程,以及與該課程相關的先修科目設計如表一:
| Course name | Prerequisites |
|---|---|
| Programming I(程式設計 I) | None |
| Discrete Mathematics(離散數學) | None |
| Data Structures(資料結構) | Programming I, Discrete Mathematics |
| Calculus I(微積分 I) | None |
| Calculus II(微積分 II) | Calculus I |
| Linear Algebra(線性代數) | Calculus II |
| Analysis of Algorithm(演算法分析) | Data Structures, Linear Algebra |
| Assembly Language(組合語言) | Data Structures |
| Operating Systems(作業系統) | Analysis of Algorithm, Assembly Language |
| Programming Language(程式語言) | Analysis of Algorithm |
| Compiler Design(編譯器設計) | Programming Language |
| Artificial Intelligence(人工智慧) | Analysis of Algorithm |
| Computational Theory(計算機理論) | Analysis of Algorithm |
| Parallel Algorithms(平行演算法) | Computational Theory |
| Numerical Analysis(數值方法) | Calculus II |
表一:某計算機科學學位之必修課程表
第一眼或許不太容易立即由表格獲得修課順序的資訊,因為表格受限於上至下、左至右的格式,只能逐項列出資訊,不容易表達資料與資料間的「先後關係」。
現在換個方式,將具有先後修課順序的課程以線段與箭號連接,若A是B的先修課程,則箭號由A指向B,即可將表一轉換成圖一:

圖一。
由圖一,將資料與資料的「先後關係」以「資料節點」與「線段(箭號)」表示,攻讀這門計算機科學學位的修課流程圖便一目了然。
這樣的想法,不只是將表格轉換成對人類視覺上有意義的「圖」而已,對電腦來說,由於以Graph建立之模型能夠保持資料之間的「關係」,使得各種巧妙的演算法能夠在Graph中完成各種任務。
(反例:若要把在Graph上實現的各種演算法,如法炮製在以二維陣列表示的表一上,將會非常困難。)
本篇文章的重點著重在介紹Graph(圖)的定義與實現方式,而接下來的文章將介紹一些基本的與Graph相關之演算法。
Graph的定義
在圖一中,每一門課程被視為「資料節點」,且課程與課程之間有「線段(箭號)」連結:
- vertex:稱每一個「資料節點」為vertex(或是node),並定義所有的vertex所形成之集合(Set)為\(V\)或\(V(G)\);
- edge:稱每一個「線段(箭號)」為edge(實際上是用一對vertex表示edge,例如\((V_i,V_j)\)即為連結Vi與Vj的edge),並定義所有的edge所形成之集合(Set)為\(E\)或\(E(G)\);
則Graph定義為\(V\)與\(E\)所形成的集合,表示成\(G(V,E)\)。
再根據edge是否具有「方向性」,可以將Graph分成「directed graph(有向圖)」與「undirected graph(無向圖)」:
- directed graph(有向圖):edge的方向性表示資料間的關係,若vertex(A)與vertex(B)之關係是「單向的」,那麼連結vertex(A)與vertex(B)的edge即具有方向性。
- 以圖一中的課程與其先修科目為例,vertex(Data Structures)是vertex(Analysis of Algorithm)的先修課程,相反則否,因此,連結兩個vertex之edge具有方向性,而所有vertex與edge形成之集合即為directed graph;
- undirected graph(無向圖):edge的方向性表示資料間的關係,若vertex(A)與vertex(B)的關係是「雙向的」,那麼連結vertex(A)與vertex(B)之edge就不具有方向性。
- 如圖二中,如果可以開車從玉山抵達太魯閣,就能夠從太魯閣原路折返回到玉山,因此,這兩個地理位置之間的交通路線便不具有方向性。

圖二:Google Map路線規劃,開車過去要4小時34分鐘。
再看幾個Graph的範例。
圖三(a)中的G1與G2為undirected graph,圖三(b)中的G3與G4為directed graph。

圖三(a):undirected graph(無向圖)。
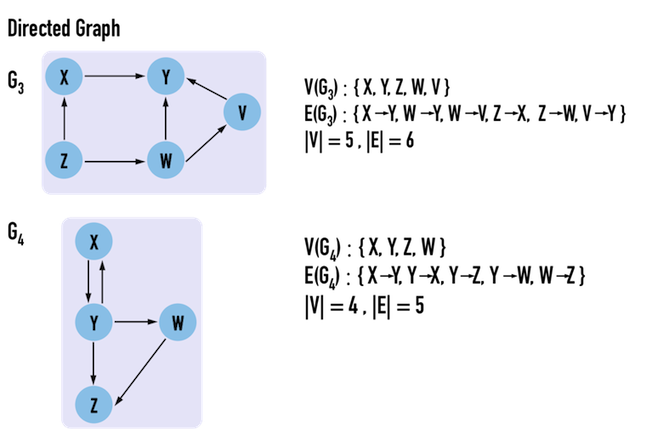
圖三(b):directed graph(有向圖)。
表示法(representation)
那麼該如何表示Graph呢?
一般有兩種常用的表示法:
- Adjacency Matrix(相鄰矩陣):一個二維矩陣,若從vertex(A)到vertex(B)有edge,則矩陣位置[A][B]值為\(1\),反之,則為\(0\)。
- 以圖四為例,在undireced graph中,vertex(X)與vertex(Y)之間有edge,則矩陣位置[X][Y]與[Y][X]之值皆為\(1\);
- 在directed graph中,有從vertex(X)指向vertex(Y)的edge,則矩陣位置[X][Y]之值為\(1\),但是沒有反向的edge,因此矩陣位置[Y][X]之值為\(0\)。
- Adjacency List(相鄰串列):先以一個一維陣列列出所有的vertex,再以Linked list表示所有與vertex相連的vertex。
(vertex接進Linked list的順序不重要,因為是Graph是定義成Set。)- 以圖四為例,在undireced graph中,vertex(W)與vertex(Z)、vertex(Y)、vertex(V)具有edge相連,則在一維陣列中表示vertex(W)之位置之後,依序接上vertex(Z)、vertex(Y)、vertex(V)。
- 在direced graph中,vertex(W)僅僅剩下指向vertex(Y)與vertex(V)的edge,因此,在一維陣列中表示vertex(W)之位置之後,只要接上vertex(Y)與vertex(V)。

圖四:Adjacency Matrix與Adjacency List適用於directed graph與undirected graph。
比較兩者的差異:
- 使用記憶體空間:
- Adjacency Matrix:一定會用到\(O(|V|^2)\),因此,若Graph較為「稠密(dense)」,各vertex之間的edge數量較多則適合使用Adjacency Matrix;
- Adjacency List:將使用\(O(|V|+|E|)\),因此,若Graph較為「稀疏(sparse)」,edge數量較少,如圖一的Graph,即適合使用Adjacency List。
- 存取資料:
- Adjacency Matrix:由於Matrix是連續記憶體,在存取資料時會稍微快一些;
- Adjacency List:同理,若是使用動態記憶體配置建立Linked list,則資料存取會稍慢(這項缺點可以使用C++的STL::Vector解決,不過STL::Vector不適合用在動態改變的Graph上)。
- 新增edge:
- Adjacency Matrix:在Matrix中增加一條edge僅僅是把矩陣中相對應位置的值從\(0\)設成\(1\),只需要\(O(1)\);
- Adjacency List:若每次都把新的vertex加在List的最前端(front),也只需要\(O(1)\)。不過,最壞情況(worst case)發生在「某個vertex與其他vertex全部相連」,因此需要\(O(|E|)\)。
- 刪除edge:
- Adjacency Matrix:在Matrix中刪除edge僅僅是把矩陣中相對應位置的值從\(1\)設成\(0\),只需要\(O(1)\);
- Adjacency List:如同在Linked list中刪除資料,需要\(O(|E|)\)。
一些名詞解釋
- adjacent(相鄰):若在vertex(A)與vertex(B)之間有一條edge(不論是否具有方向性),則稱vertex(A)與vertex(B)為adjacent(相鄰)。
- subgraph(子圖):若構成G'的兩個集合滿足\(V(G')\subseteq V(G), E(G')\subseteq E(G)\),則稱G'為G的subgraph,如圖五。

圖五:G與G的subgraph。
- path(路徑):若從vertex(V1)到vertex(Vk)存在一連串前後相接的edge(\((V_i,V_{i+1})\subseteq E(G),i=1,2,...,k-1\)),則稱這一連串edge為「從vertex(V1)到vertex(Vk)的path」。
- length(長度)/distance(距離):length(或distance)即是path中的edge數。
- simple path(簡單路徑):若一條path中,除了起點vertex與終點vertex之外,沒有vertex被重複經過,則稱這條path為simple path。
- 如圖六中,path:X-Y-Z即為simple path,path:W-Y-Z-V-W也是simple path,即使W有重複,但是因為分別是起點與終點,所以仍符合定義。而path:Y-X-Y-W就不是simple path,因為第二次經過Y時,Y不是終點。

圖六:。
- cycle(循環):若有ㄧ條「simple path」的起點vertex與終點vertex相同,則稱這條path為cycle。
- 圖六中的path:W-Y-Z-V-W,稱為directed cycle(有向循環);
- 圖七中的path:Y-V-W-Y與path:X-Y-W-Z-X皆為undirected cycle(無向循環)。
- acyclic graph(無循環圖):若graph中不存在cycle,則稱這個graph為acyclic graph,見圖七。
- 在Tree中找不到任何一條simple path的起點與終點是相同vertex(node),因此Tree一定是acyclic graph。

圖七:。
- weight(權重):若要表示兩個地理位置之間的「距離」或是運送「成本」,可以在edge上加上weight,這樣的graph又稱為weighted graph,如圖八。

圖八:weight的值可能為正或是負。
- connected:若存在從vertex(A)指向vertex(B)、以及從vertex(B)指向vertex(A)的edge(若是在directed graph中,需要兩條edge;若是undirected graph只需要一條edge),則稱vertex(A)與vertex(B)為connected,見圖九(a)。

圖九(a):。
- connected in undirected graph:若在undirected graph中,對任意兩個vertex都存在一條path連結這兩個vertex,則稱此undirected graph是connected。
- 圖九(b)中,G1中的所有vertex都可以經過一條path到達其他vertex,因此G1為connected。
- G2中,vertex:X、S、Z分別與vertex:Y、W、T之間皆不存在path,因此G2不是connected。
- connected component:若在一個undirected graph中,存在某一個subgraph是connected,而且沒有任何vertex、edge再加入這個subgraph之集合後仍能使得這個subgraph維持connected特性,則稱此subgraph為connected component(最大集合的connected subgraph)。
- 圖九(b)中,右上方為G1的其中一個subgraph。此subgraph不是connected component,原因在於,再加入vertex:W、T,以及edge:(Y,W)、(Y,T),也就是變回G1後,仍然維持connected特性,因此這個subgraph並不是「可以維持connected的最大集合」。
換句話說,在一個connected的undirected graph中,只會有一個connected component,就是graph本身。 - 圖九(b)的G2本身不是connected,而是由兩個connected component組成。
- 圖九(b)中,右上方為G1的其中一個subgraph。此subgraph不是connected component,原因在於,再加入vertex:W、T,以及edge:(Y,W)、(Y,T),也就是變回G1後,仍然維持connected特性,因此這個subgraph並不是「可以維持connected的最大集合」。

圖九(b):。
- strongly connected in directed graph:若在directed graph中,對任意兩個vertex(A)與vertex(B)同時存在「從vertex(A)走到vertex(B)」以及「從vertex(B)走到vertex(A)」的path,則稱此directed graph是strongly connected。
- 圖九(c),G3中的所有vertex都可以經過一條path到達其他vertex,因此G3為strongly connected。
- G4並非strongly connected,例如,雖然path:S-X-T-Z可以從vertex(S)走到vertex(Z),但是從vertex(Z)卻無法經由任何一條path到達vertex(S)。
- strongly connected component:若在一個directed graph中,存在某一個subgraph是strongly connected,而且沒有任何vertex、edge再加入這個subgraph之集合後仍能使得這個subgraph維持strongly connected特性,則稱此subgraph為strongly connected component(最大集合的strongly connected subgraph)。
- 圖九(c)中,右上方為G3的其中一個subgraph。此subgraph不是strongly connected component,原因在於,再加入edge:(W,Z)後(也就是變回G3),仍然維持connected特性,因此這個subgraph並不是「可以維持connected的最大集合」。
如同undirected graph,若一個directed graph本身是strongly sonnected,則本身也是唯一的strongly connected component。 - G4是由三個strongly connected component組成。
- 圖九(c)中,右上方為G3的其中一個subgraph。此subgraph不是strongly connected component,原因在於,再加入edge:(W,Z)後(也就是變回G3),仍然維持connected特性,因此這個subgraph並不是「可以維持connected的最大集合」。

圖九(c):。
- self-loop(自我迴圈):若有edge從vertex(A)指向vertex(A),即稱為self-edge或是self-loop。
- multigraph(多邊圖):若在graph中相同的edge重複出現多次,則稱此圖為multigraph,之後要討論的Graph將排除此種情形。

圖十:self-loop與multigraph在directed graph和undirected graph中定義皆相同。
預告:Graph的應用
在接下來的文章,主要將探討以下三個應用的演算法:
-
Minimum Spanning Tree(MST,最小生成樹):給定一個connected、weighted的undirected graph,要在這個graph中,找到(1)連結所有vertex,而且(2)edge上的weight總和最小的「Tree」。
例如,鄉公所要鋪路,先以鄉公所為中心(root),把所有馬路必須到達的地區視為vertex,則路就是edge,那麼,鋪路的目標便是利用最低成本(weight總和最小)將馬路延伸到所有必須抵達的地區,這就是MST的問題。 -
Shortest Path(最短路徑):顧名思義,最短路徑即是找到vertex(A)與vertex(B)之間「成本」最小的path,例如以Google Map規劃時間成本最小的路線。
其中又可以分為:- Single-Pair Shortest Path:從一個vertex,抵達特定的另一個vertex之最短路徑;
- Single-Source Shortest Path:從一個vertex,抵達graph中其餘所有vertex之最短路徑;
- Single-Destination Shortest Path:從每一個graph中的vertex抵達特定的vertex之最短路徑;
- All-Pairs Shortest Path:graph中的所有vertex抵達其餘所有vertex之最短路徑。
-
Network Flow(網路流):若現在有一個複雜的水管系統,水從入水口流入,經過許多互相連結、且孔徑不一的水管後,從出水口流出,目標是一次流入最大量的水。
其中可能遇到的問題如:由於水管的孔徑各不相同,若先流過一條半徑只有2公分的水管,則接在其後的水管的半徑即使再大,水流量仍會被半徑2公分的水管所限制,因此整體流量也就受限制。
如何分配水流在水管之間的流法,即是Network Flow要處理的問題。
不過在介紹以上三項主題之前,下兩篇文章將先介紹在Graph中最基本的搜尋(Search)方法:
- Breadth-First Search(BFS,廣度優先搜尋),與
- Depth-First Search(DFS,深度優先搜尋)。
參考資料:
- Introduction to Algorithms, Ch22
- Fundamentals of Data Structures in C++, Ch6
- Hacker Earth:Graph Theory - Part I
- Theory of Programming:Graph Theory Basics
- Wikipedia:Tree(graph theory)
- Wikipedia:Shortest path problem
- Google Map:從玉山國家公園到太魯閣國家公園
Graph系列文章
Graph: Intro(簡介)
Graph: Breadth-First Search(BFS,廣度優先搜尋)
Graph: Depth-First Search(DFS,深度優先搜尋)
Graph: 利用DFS和BFS尋找Connected Component
Graph: 利用DFS尋找Strongly Connected Component(SCC)
Graph: 利用DFS尋找DAG的Topological Sort(拓撲排序)
Minimum Spanning Tree:Intro(簡介)
Minimum Spanning Tree:Kruskal's Algorithm
Minimum Spanning Tree:Prim's Algorithm
Minimum Spanning Tree:Prim's Algorithm using Min-Priority Queue
Shortest Path:Intro(簡介)
Single-Source Shortest Path:Bellman-Ford Algorithm
Single-Source Shortest Path:on DAG(directed acyclic graph)
Single-Source Shortest Path:Dijkstra's Algorithm
All-Pairs Shortest Path:Floyd-Warshall Algorithm
Flow Networks:Maximum Flow & Ford-Fulkerson Algorithm
回到目錄: