Minimum Spanning Tree：Intro(簡介)

先備知識與注意事項

本篇文章旨在介紹Graph中常見的應用：Minimum Spanning Tree(MST，最小生成樹)。

在介紹演算法時，繼續會用上Set(集合)的概念，如果對Set有基本概念，相信讀者一定可以躺著讀完這篇。

目錄

• Minimum Spanning Tree(MST，最小生成樹)
• 演算法概念(Generic Algorithm)
  • Theorom1
  • 證明：Theorem1
  • Corollary2
• 參考資料
• MST系列文章

Minimum Spanning Tree(MST，最小生成樹)

圖一(a)。

考慮一個connected、weighted的undirected graph，如圖一(a)，在Graph上能夠定義Spanning Tree為：

• 連結所有Graph中的vertex的樹，見圖一(b)。
• 因為是樹，所以沒有cycle。
• 因為是樹，若Graph有\(V\)個vertex，Spanning Tree只有\(|V|-1\)條edge。

圖一(b)。

由於Graph具有weight，因此，不同的Spanning Tree，可能有不同的weight總和，而其中，具有最小weight總和的樹，稱為Minimum Spanning Tree(MST)，如圖一(c)。

圖一(c)。

小小提醒：

• 由於Graph的weight只要求要是實數(real value)，而且不要求每一條edge的weight必須唯一，因此，Graph中的MST可能不唯一。
• 由於MST的定義只要求「最小weight總和」，因此root是哪個vertex、樹是否平衡、height(樹高)是否夠小等等問題，皆不在必要的考慮範圍內。

演算法概念(Generic Algorithm)

根據MST的定義，MST一定要包含Graph中的所有vertex，而且要使得連結所有vertex的edge之weight總和最小，所以，關鍵便是「如何挑選edge」。

尋找MST的演算法之大方向如下：
(此即為下兩篇文章將介紹的Kruskal's Algorithm與Prim's Algorithm的心法口訣)

• 建立一個用來收集/表示「所有MST中的edge」之集合，稱為Set A。見圖二(a)。
• Set A起初是空集合，演算法將逐一挑選出「滿足MST」之edge，並利用Union(聯集)把edge視為element放進Set A中。見圖二(b)。
• 因此，Set A會是一個逐漸長大的MST之edge的subset(子集合)，\(A\subseteq E(MST)\)。
• 演算法完成後，Set A就包含了所有MST的edge。見圖二(c)。

圖二(a)。

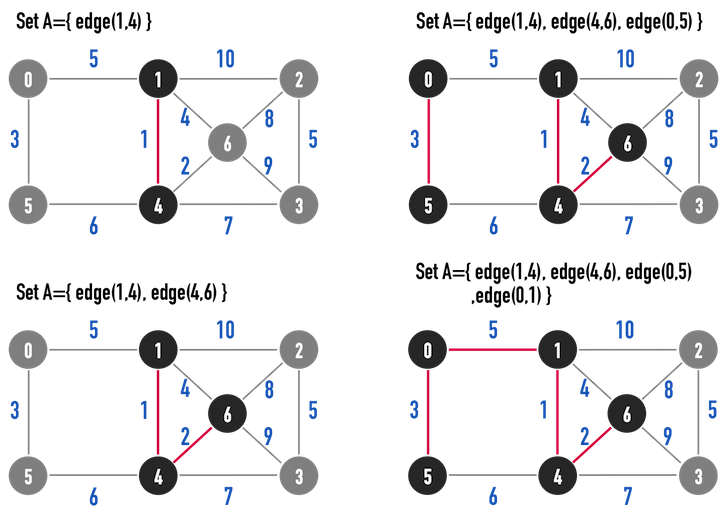
圖二(b)。

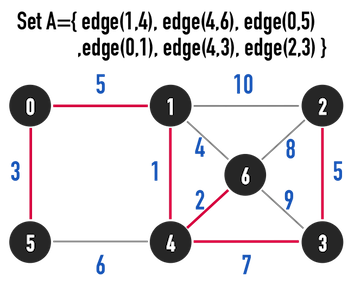
圖二(c)。

接著將介紹一個定理(theorem)與其等價的推論(corollary)，來說明怎麼樣的edge對Set A來說是安全的(safe)，使得「該edge加入Set A後，Set A仍然滿足\(A\subseteq E(MST)\)」。

先定義四個名詞概念：

• Cut：Cut \((S,V-S)\)是一種將Graph(\(G=(V,E)\))的V(vertex set)分成兩部分的partition(分割)。
  • 圖三(a)左，Cut \((S,V-S)\)將Graph中的vertex分割出兩個Set，\(S=\){\(1,4\)}，\(V-S=\){\(0,2,3,5,6\)}。
  • 圖三(a)右，Cut \((S,V-S)\)將Graph中的vertex分割出兩個Set，\(S=\){\(1,4,6,0,5\)}，\(V-S=\){\(2,3\)}。

圖三(a)。

• cross：若存在一條edge(X,Y)，其中\(X\subseteq S\)，\(Y\subseteq V-S\)，則稱這條edge「crosses」Cut \((S,V-S)\)。
  • 把圖三(a)左圖調整成圖三(b)，觀察出edge(1,0)、edge(1,2)、edge(1,6)、edge(4,3)、edge(4,5)、edge(4,6)對Cut而言，都是crossing edge。

圖三(b)。

• respect：若Set A中沒有任何一條edge是Cut的crossing edge，則稱這個Cut「respect」Set A。(因為尊敬，所以不切開。)
  • 以圖三(b)為例，Set A\(=\){\(edge(1,4)\)}，vertex(1)與vertex(4)都在\(S=\){\(1,4\)}裡，因此edge(1,4)不是Cut \((S,V-S)\)的crossing edge，則稱Cut \((S,V-S)\)「respect」Set A。
• light edge：在考慮範圍內，「weight最小」的edge稱為light edge。
  • 以圖三(b)為例，若考慮所有的crossing edge，則edge(4,6)即為light edge。
  • 如果有多條edge的weight都相同，並且為極小值，那麼light edge將不止一條。

以上專有名詞有點多，最重要的是釐清：

• Set A是edge的集合；
• Cut的兩個Set：\((S,V-S)\)是vertex的集合。
  
  

Theorom1

(對應Introduction to Algorithms第23章，Theorem 23.1)

Theorem1要說的是，給定：

1. Graph \(G=(V,E)\)是一個connected、weighted、undirected graph；
2. Set A是MST之edge的subset，\(A\subseteq E(MST)\)；
3. Cut \((S,V-S)\) 必須「respect」Set A；
4. edge(X,Y)是crossing edge，也是light edge；

那麼，edge(X,Y)對Set A即為安全的(safe)，將edge(X,Y)加入Set A後，Set A必定能夠滿足\(A\subseteq E(MST)\)。
換句話說，edge(X,Y)一定會是MST的edge。

以圖四(a)為例，確認前三項條件皆滿足，並且找到所有crossing edge中weight最小的edge為edge(4,6)，則edge(4,6)必定是MST的edge。

圖四(a)。

證明：Theorem1

如圖五(a)，考慮一個connected、weighted、undirected graph上的MST：

• MST以T表示，\(T=(V(T),E(T))\)；
  • 以圖五(a)為例，\(E(T)=A\cup edge(Z,W)\cup edge(A,C)\)；
• Set A為T的edge之subset；
  • 以圖五(a)為例，\(A=\){\(edge(X,Z),edge(Y,W),edge(W,B),edge(W,C)\)}；
• Cut \((S,V-S)\)可以是任意「respect」Set A的Cut，並假設edge(X,Y)是Cut上所有crossing edge中的light edge，而且edge(X,Y)不屬於T；
  • 圖五(a)中，找到Cut \((S,V-S)\)，其中 \(S=\){\(X,Z\)}，\(V-S=\){\(Y,W,B,C,A\)}，edge(X,Y)為light edge；
• 由於Cut「respect」Set A，因此edge(X,Y)不在Set A裡面。

圖五(a)。

因為MST是一個Tree，所以T上的各個vertex之間只存在唯一的path，因此，vertex(Y)到vertex(X)之間，必定在T上存在一條path，而且這條path中，將有一條edge會是Cut的crossing edge，令這條crossing edge為edge(Z,W)。
同樣地，由於Cut「respect」Set A，edge(Z,W)也不會在Set A裡面。

又因為edge(X,Y)是所有crossing edge中的light edge，所以：\(weight(X,Y)\leq weight(Z,W)\)。

此時，如果把edge(Z,W)從T中移除，T將分成兩個connected component，見圖五(b)。

• 因為edge(Z,W)不在Set A裡面，這兩個connected component的全部edge所形成之集合必定包含Set A。

再將這兩個connected component接上edge(X,Y)，形成一棵新的Tree，稱為T'，其中 \(E(T')=E(T)-edge(Z,W)+edge(X,Y)\)。

圖五(b)。

因為\(weight(X,Y)\leq weight(Z,W)\)，便得到：

• \(weight(T')\leq weight(T)-weight(Z,W)+weight(X,Y)\)；
  \(weight(T')\leq weight(T)\)；

因此，若T是MST，那麼T'也會是一棵MST。

• 以圖五(b)為例，經過\(E(T')=E(T)-edge(Z,W)+edge(X,Y)\)後，新的\(E(T')=\){\(A+edge(X,Y)+edge(A,C)\)}。

因為Set A與edge(X,Y)同屬於MST的edge之集合，因此edge(X,Y)對Set A會是安全的(safe)，使得edge(X,Y)加入Set A後，Set A仍然能夠滿足\(A\subseteq E(MST)\)。(證明完畢)

Corollary2

(對應Introduction to Algorithms第23章，Corollary 23.2)

與Theorem1等價的Corollary2要說的是，給定：

1. Graph \(G=(V,E)\)是一個connected、weighted、undirected graph；
2. Set A是MST之edge的subset，\(A\subseteq E(MST)\)；
3. subgraph \(C=(V_C,E_C)\)為「Forest \(G_A=(V,A)\)」中的connected component，C可以視為一棵Tree；
4. edge(X,Y)是所有在「Forest \(G_A=(V,A)\)」中，連結各個connected component的light edge；

那麼，edge(X,Y)對Set A也會是安全的(safe)，將edge(X,Y)加入Set A後，Set A必定能夠滿足\(A\subseteq E(MST)\)。

以圖四(b)為例，\(G_A=(V,A)\)裡有兩個connected component，分別為：

• \(C_1=(V_1,E_1)\)，其中\(V_1=\){\(0,5\)}，\(E_1=\){\(edge(0,5)\)}；
• \(C_2=(V_2,E_2)\)，其中\(V_2=\){\(1,4,6\)}，\(E_2=\){\(edge(1,4), edge(4,6)\)}。

根據Theorem1，若Cut \((C_1,V-C_1)\)「respect」Set A，那麼Cut上的「crossing light edge」，一定也是MST的edge。

觀察圖四(b)，顯然，Set A中的edge都沒有「cross」Cut \((C_1,V-C_1)\)，而所有crossing edge中的light edge為edge(0,1)，因此，能夠將edge(0,1)加入Set A。

圖四(b)。

關於MST的應用，筆者也還在摸索，這裡就放上兩個連結供讀者參考：

• GeeksforGeeks：Applications of Minimum Spanning Tree Problem。
• T. M. Murali：Applications of Minimum Spanning Tree Problem。

接下來，將以兩篇文章的篇幅介紹尋找MST的演算法：Kruskal's Algorithm與Prim's Algorithm。

Kruskal's Algorithm與Prim's Algorithm都屬於Greedy Algorithm，簡單來說，就是「追求當前的最佳情況，並期望所有最佳的當前情況，能夠歸結出最終的最佳情況」。
在尋找MST的問題中，最佳情況就是「挑選weight最小的edge」，並期望透過每一次都挑選weight最小之edge，最後能得到總和weight最小的MST。
這兩個演算法將以皆滿足Theorem1與Corollary2但不同的策略挑選edge，並且最後都能得到Graph上的MST。

參考資料：

• Introduction to Algorithms, Ch23
• Fundamentals of Data Structures in C++, Ch6
• Rashid Bin Muhammad：Generic-Minimum Spanning Tree
• GeeksforGeeks：Applications of Minimum Spanning Tree Problem
• T. M. Murali：Applications of Minimum Spanning Tree Problem

MST系列文章

Minimum Spanning Tree：Intro(簡介)
Minimum Spanning Tree：Kruskal's Algorithm
Minimum Spanning Tree：Prim's Algorithm
Minimum Spanning Tree：Prim's Algorithm using Min-Priority Queue

回到目錄：

目錄：演算法與資料結構