先備知識與注意事項
在上一篇文章Minimum Spanning Tree:Intro(簡介)介紹過MST的問題情境以及演算法概念,這篇文章要接著介紹尋找MST的演算法之一:Kruskal's Algorithm。
說明演算法時將會用上專有名詞如「light edge」、「cross」,如果不太熟悉,可以參考上一篇文章。
Kruskal's Algorithm將會用到Set的概念來收集MST中的edge,建議讀者可以先閱讀Set:以Array表示複習一下Set之表示法。
目錄
Kruskal's Algorithm
考慮圖二(a)的Graph,目標是要在此Graph上找到MST。

圖二(a)。
Kruskal's Algorithm之演算法將使用三個資料項目:
edgesetMST[]:用來收集所有MST中的edge,功能與Theorem1中的Set A相同。subset[]:用來記錄edgesetMST[]中的edge之兩端vertex所屬的集合,目的是用來判斷是否形成cycle。increaseWeight[]:把Graph中的edge按照weight由小到大排序,依序放進increaseWeight[],當演算法在「挑選edge」形成最短路徑時,便是按照「weight由小到大」之順序挑選。- 將圖二(a)的Graph之edge排序,可以得到如圖二(b)的
increaseWeight[]。
- 將圖二(a)的Graph之edge排序,可以得到如圖二(b)的

圖二(b)。
演算法步驟如下:
- 先把Graph中的每一個vertex都視為各自獨立且互斥的集合(disjoint set),也就是把
subset[]的每一個元素都設為\(-1\),如圖二(c)。- 負值表示每個vertex都是各自Set的root。
- \(|-1|=1\)表示每個Set裡面只有一個element。
- 從Graph中,按照「weight由小到大」之順序得到如圖二(b)的
increaseWeight[]。 - 此時
edgesetMST[]還是空集合。

圖二(c)。
接著開始進入「挑選edge」的迴圈。
首先,根據increaseWeight[](從index(\(0\))開始取得edge),整個Graph中weight最小的edge是edge(1,4),便利用FindSetCollapsing()與subset[]判斷vertex(1)與vertex(4)是否屬於同一個Set,如果不是的話,便執行:
- 將edge(1,4)加入
edgesetMST[],見圖二(d); - 並利用
UnionSet()將vertex(1)與vertex(4)合併成一個新的Set。- 因為兩個Set中的element數目相同,以何者作為合併後的Set之root不影響,便更新
subset[4]=1,subset[1]=-2。
- 因為兩個Set中的element數目相同,以何者作為合併後的Set之root不影響,便更新

圖二(d)。
根據increaseWeight[],下一個為edge(4,6),由於vertex(4)與vertex(6)屬於不同Set,便重複上述步驟:
- 將edge(4,6)加入
edgesetMST[],見圖二(e); - 並利用
UnionSet()將vertex(4)與vertex(6)合併成一個新的Set。- 因為vertex(4)所屬的Set中有2個element,vertex(6)所屬的Set只有一個element,便將vertex(6)併入vertex(4)之Set,更新
subset[6]=1,subset[1]=-3。
- 因為vertex(4)所屬的Set中有2個element,vertex(6)所屬的Set只有一個element,便將vertex(6)併入vertex(4)之Set,更新

圖二(e)。
根據increaseWeight[],下一個edge為edge(0,5),由於vertex(0)與vertex(5)屬於不同Set,便重複上述步驟:
- 將edge(0,5)加入
edgesetMST[],見圖二(f); - 並利用
UnionSet()將vertex(0)與vertex(5)合併成一個新的Set。

圖二(f)。
關鍵是下一個edge:edge(1,6)。
由於vertex(1)與vertex(6)屬於同一個Set,表示vertex(6)一定與Set中某個vertex具有edge相連(此例為vertex(4)),如果將edge(1,6)加入edgesetMST[],將會形成cycle,便違反Tree的結構。
因此,即使在所有尚未加入edgesetMST[]的edge中,edge(1,6)的weight最小,仍必須將其忽略。

圖二(g)。
到目前為止可以得到結論:只要把像是edge(1,6)這樣會使得edgesetMST[]中的vertex形成cycle的edge忽略掉,再根據increaseWeight[],依序挑選weight最小的edge,即可找到MST。
接下來的挑選過程如圖二(h)-(k)。

圖二(h)。
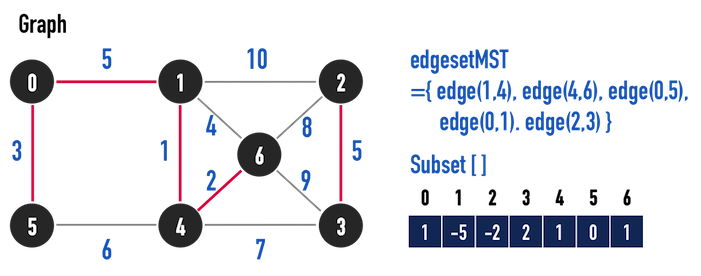
圖二(i)。
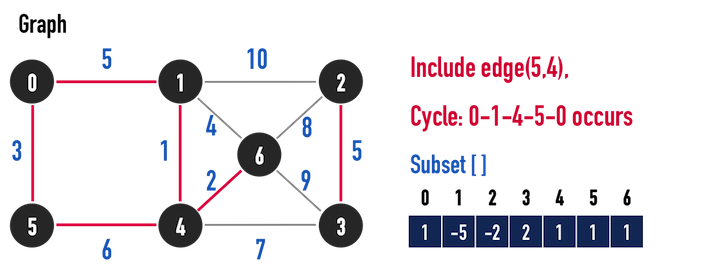
圖二(j)。
這裡有個小細節:為什麼subset[5]變成\(1\)?
因為當increaseWeight[]交出edge(5,4)作為當前具有最小weight之edge時,FindSetCollapsing()會對vertex(5)與vertex(4)執行「找到所屬的Set之root」,以及「把vertex之parent/predecessor指向root」,所以vertex(5)會因為「塌陷(Collapsing)」的關係,subset[5]被更新成vertex(1)。
這使得往後在尋找「vertex(5)所屬之Set」時,只要\(O(1)\)的時間複雜度。

圖二(k)。
如圖二(k),當edgesetMST[]加入edge(4,3)後,MST便尋找完畢。
用肉眼看起來,除了weight\(=4\)的edge(1,6),與weight\(=6\)的edge(5,4)之外,確實是Graph上具有較小weight之edge都被挑進MST了。
但是要怎麼驗證Kruskal's Algorithm不是運氣好呢?
答案就在上一篇文章提到的Theorem1與Corollary2裡面。
根據Corollary2,給定:
- Graph \(G=(V,E)\)是一個connected、weighted、undirected graph;
- Set A是MST之edge的subset,\(A\subseteq E(MST)\);
- subgraph \(C=(V_C,E_C)\)為「Forest \(G_A=(V,A)\)」中的connected component,C可以視為一棵Tree;
- edge(X,Y)是所有在「Forest \(G_A=(V,A)\)」中,連結各個connected component的light edge;
那麼,edge(X,Y)對Set A也會是安全的(safe),將edge(X,Y)加入Set A後,Set A必定能夠滿足\(A\subseteq E(MST)\)。
再看看Kruskal's Algorithm,演算法一開始會將所有vertex都視為各自獨立且互斥的Set,因此,每一個vertex都可以視為一個connected component,那麼,在所有連結connected component的edge(也就是連結各個vertex的edge)當中的light edge,就必定是MST的edge。
因此,Kruskal's Algorithm按照「weight由小到大」的順序挑選edge,並且避免產生cycle,即可找到MST。
程式碼
以下的程式範例包含了struct Edge、class Graph、Set相關函式與main()。
struct Edge:因為edgesetMST[]與increaseWeight[]需要同時儲存edge的兩個端點vertex與weight,因此建立一個struct結構表示edge。
class Graph:與BFS/DFS系列中的class Graph不同的是,這裡使用了Adjacency Matrix而不是Adjacency List。
(為節省篇幅長度,與BFS/DFS相關的member(包含data和funtion)暫時隱藏。)
KruskalMST()為主要演算法,內容如前一節所介紹。
GetSortedEdge()是為了得到increaseWeight[],其中利用了C++標準函式庫(STL)的sort(),因此有個自行定義的WeightComp(),用來比較兩條edge之weight大小。
(關於STL的sort(),請參考:Cplusplus:std::sort())
與Set有關的兩個函式FindSetCollapsing()與UnionSet()內如也如本篇文章第一小節所介紹。
最後,main()利用AddEdge()建立出Graph的AdjMatrix,並執行KruskalMST()。
// C++ code
#include <iostream>
#include <vector>
#include <list>
#include <iomanip> // for setw()
struct Edge{
int from, to, weight;
Edge(){};
Edge(int u, int v, int w):from(u), to(v), weight(w){};
};
class GraphMST{
private:
int num_vertex;
std::vector<std::vector<int>> AdjMatrix;
public:
GraphMST():num_vertex(0){};
GraphMST(int n):num_vertex(n){
AdjMatrix.resize(num_vertex);
for (int i = 0; i < num_vertex; i++) {
AdjMatrix[i].resize(num_vertex);
}
}
void AddEdge(int from, int to, int weight);
void KruskalMST();
void GetSortedEdge(std::vector<struct Edge> &vec);
friend int FindSetCollapsing(int *subset, int i);
friend void UnionSet(int *subset, int x, int y);
};
int FindSetCollapsing(int *subset, int i){ // 用遞迴做collapsing
int root; // root
for (root = i; subset[root] >= 0; root = subset[root]);
while (i != root) {
int parent = subset[i];
subset[i] = root;
i = parent;
}
return root;
}
void UnionSet(int *subset, int x, int y){
int xroot = FindSetCollapsing(subset, x),
yroot = FindSetCollapsing(subset, y);
// 用rank比較, 負越多表示set越多element, 所以是值比較小的element比較多
// xroot, yroot的subset[]一定都是負值
if (subset[xroot] <= subset[yroot]) { // x比較多element或是一樣多的時候, 以x作為root
subset[xroot] += subset[yroot];
subset[yroot] = xroot;
}
else { // if (subset[xroot] > subset[yroot]), 表示y比較多element
subset[yroot] += subset[xroot];
subset[xroot] = yroot;
}
}
bool WeightComp(struct Edge e1, struct Edge e2){
return (e1.weight < e2.weight);
}
void GraphMST::GetSortedEdge(std::vector<struct Edge> &edgearray){
for (int i = 0; i < num_vertex-1; i++) {
for (int j = i+1; j < num_vertex; j++) {
if (AdjMatrix[i][j] != 0) {
edgearray.push_back(Edge(i,j,AdjMatrix[i][j]));
}
}
}
// 用std::sort 排序, 自己定義一個comparison
std::sort(edgearray.begin(), edgearray.end(), WeightComp);
}
void GraphMST::KruskalMST(){
struct Edge *edgesetMST = new struct Edge[num_vertex-1];
int edgesetcount = 0;
int subset[num_vertex];
for (int i = 0; i < num_vertex; i++) {
subset[i] = -1;
}
std::vector<struct Edge> increaseWeight;
GetSortedEdge(increaseWeight); // 得到排好序的edge的vec
for (int i = 0; i < increaseWeight.size(); i++) {
if (FindSetCollapsing(subset, increaseWeight[i].from) != FindSetCollapsing(subset, increaseWeight[i].to)) {
edgesetMST[edgesetcount++] = increaseWeight[i];
UnionSet(subset, increaseWeight[i].from, increaseWeight[i].to);
}
}
// 以下僅僅是印出vertex與vertex之predecessor
std::cout << std::setw(3) << "v1" << " - " << std::setw(3) << "v2"<< " : weight\n";
for (int i = 0; i < num_vertex-1; i++) {
std::cout << std::setw(3) << edgesetMST[i].from << " - " << std::setw(3) << edgesetMST[i].to
<< " : " << std::setw(4) << edgesetMST[i].weight << "\n";
}
}
void GraphMST::AddEdge(int from, int to, int weight){
AdjMatrix[from][to] = weight;
}
int main(){
GraphMST g6(7);
g6.AddEdge(0, 1, 5);g6.AddEdge(0, 5, 3);
g6.AddEdge(1, 0, 5);g6.AddEdge(1, 2, 10);g6.AddEdge(1, 4, 1);g6.AddEdge(1, 6, 4);
g6.AddEdge(2, 1, 10);g6.AddEdge(2, 3, 5);g6.AddEdge(2, 6, 8);
g6.AddEdge(3, 2, 5);g6.AddEdge(3, 4, 7);g6.AddEdge(3, 6, 9);
g6.AddEdge(4, 1, 1);g6.AddEdge(4, 3, 7);g6.AddEdge(4, 5, 6);g6.AddEdge(4, 6, 2);
g6.AddEdge(5, 0, 3);g6.AddEdge(5, 4, 6);
g6.AddEdge(6, 1, 4);g6.AddEdge(6, 2, 8);g6.AddEdge(6, 3, 9);g6.AddEdge(6, 4, 2);
std::cout << "MST found by Kruskal:\n";
g6.KruskalMST();
return 0;
}
output:
MST found by Kruskal:
v1 - v2 : weight
1 - 4 : 1
4 - 6 : 2
0 - 5 : 3
0 - 1 : 5
2 - 3 : 5
3 - 4 : 7
結果如同圖二(k):

圖二(k)。
以上便是利用Kruskal's Algorithm尋找MST之介紹。
下一篇文章將介紹尋找MST的另一個基本款:Prim's Algorithm。
參考資料:
- Introduction to Algorithms, Ch23
- Fundamentals of Data Structures in C++, Ch6
- Rashid Bin Muhammad:Kruskal's Algorithm
- Dickson Tsai:Disjoint Sets - Data Structures in 5 Minutes
- GeeksforGeeks:Greedy Algorithms | Set 2 (Kruskal’s Minimum Spanning Tree Algorithm)
- HackerEarth:Disjoint Set Union (Union Find)
- Cplusplus:std::sort()
MST系列文章
Minimum Spanning Tree:Intro(簡介)
Minimum Spanning Tree:Kruskal's Algorithm
Minimum Spanning Tree:Prim's Algorithm
Minimum Spanning Tree:Prim's Algorithm using Min-Priority Queue
回到目錄: