先備知識與注意事項
在Minimum Spanning Tree:Prim's Algorithm中介紹過Prim's Algorithm的概念,也提供了範例程式碼。
本篇文章將補充以稍微優秀一點的資料結構:Min-Priority Queue實現Prim's Algorithm中的「取最小值(ExtractMin)」的方法。
上一篇文章的MinKeyExtract()需要把整個key[]走過一次,時間複雜度為\(O(|V|)\),其中\(|V|\)表示vertex的數量。
而以Binary Heap實現的Min-Priority Queue,在「取最小值」的時候只要\(O(\log{|V|})\),即為以Binary Tree解讀Binary Heap的「樹高」,理論上應該會比較有效率。
建議讀者可以先閱讀以下文章,:
- Minimum Spanning Tree:Intro(簡介):MST的基本概念,以及證明用的Theorem1與Corollary2。
- Minimum Spanning Tree:Prim's Algorithm:Prim's Algorithm的基本概念。
- Priority Queue:Binary Heap:以Binary Heap實現Min-Priority Queue的方法。
目錄
Prim's Algorithm
以下不再贅述Prim's Algorithm的概念,直接以圖示觀察Min-Priority Queue的作用。
觀察圖一(a)到圖一(m):
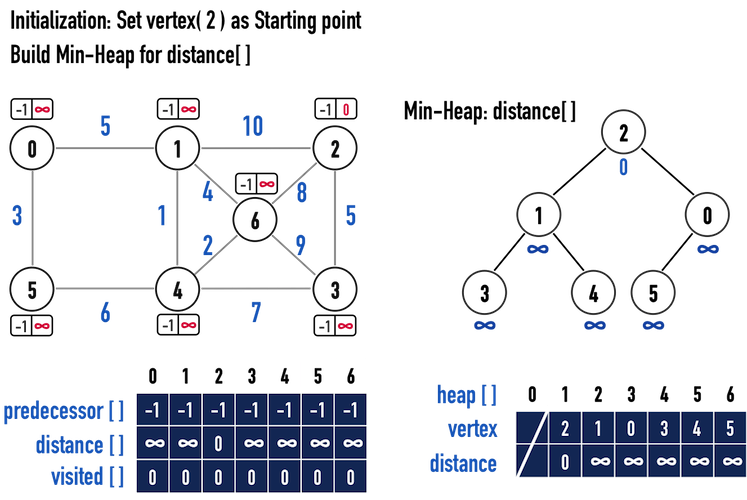
圖一(a)。
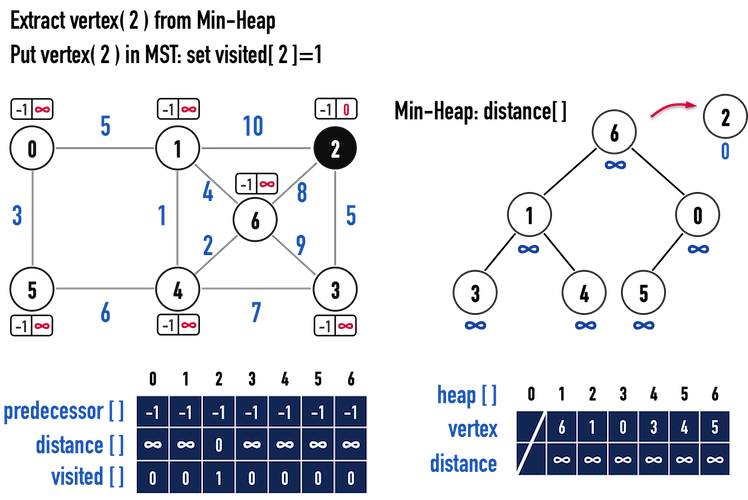
圖一(b)。
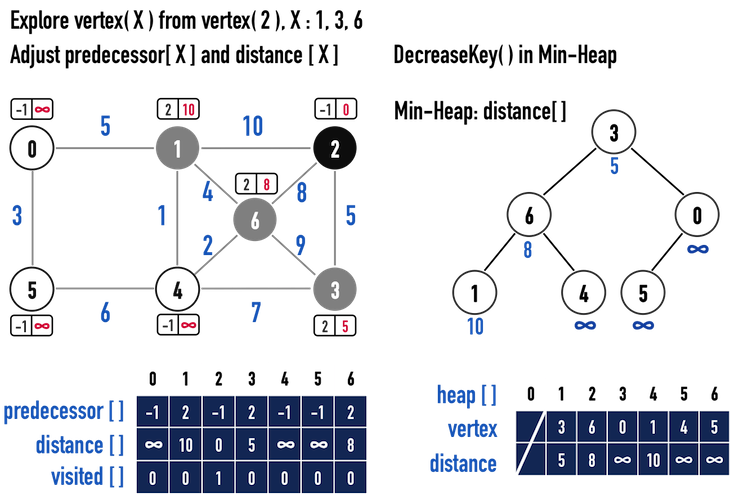
圖一(c)。
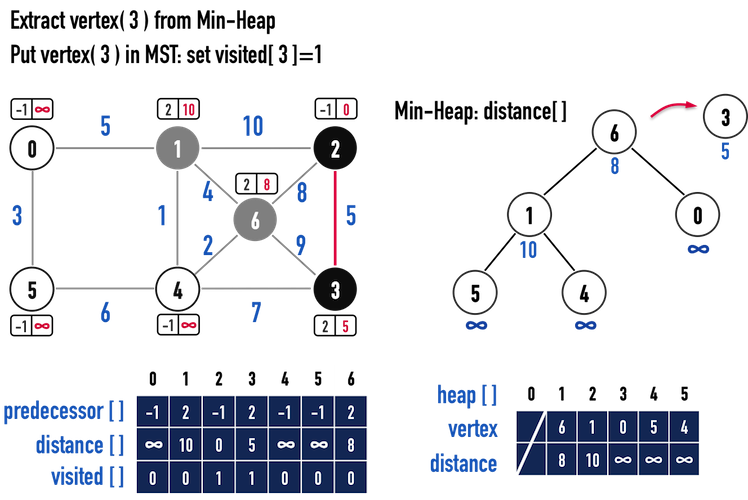
圖一(d)。
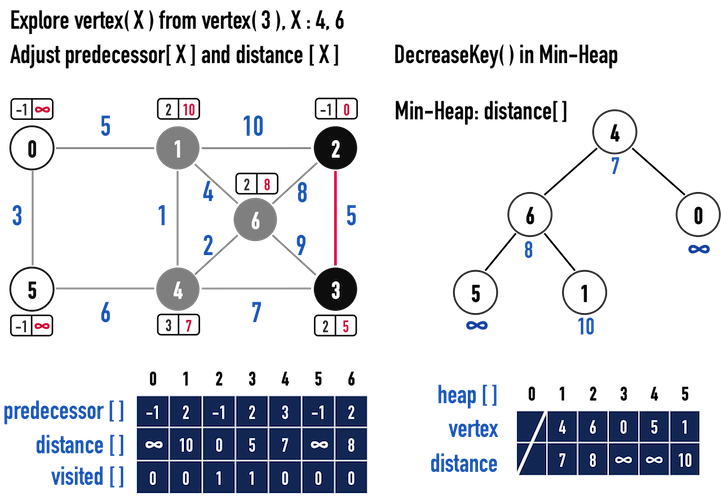
圖一(e)。
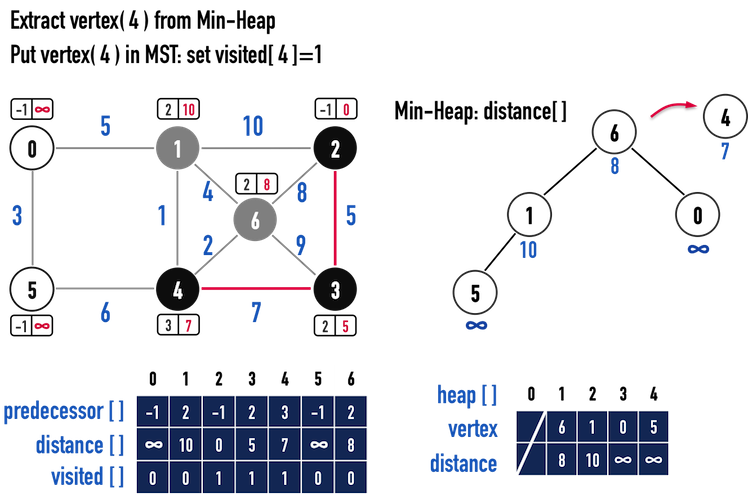
圖一(f)。
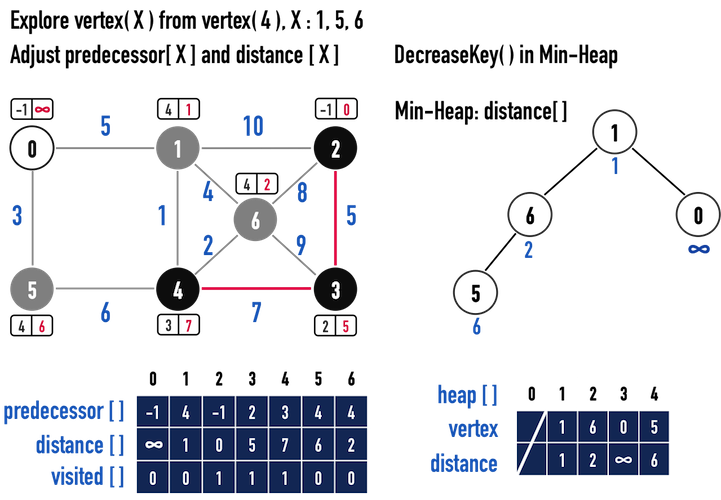
圖一(g)。
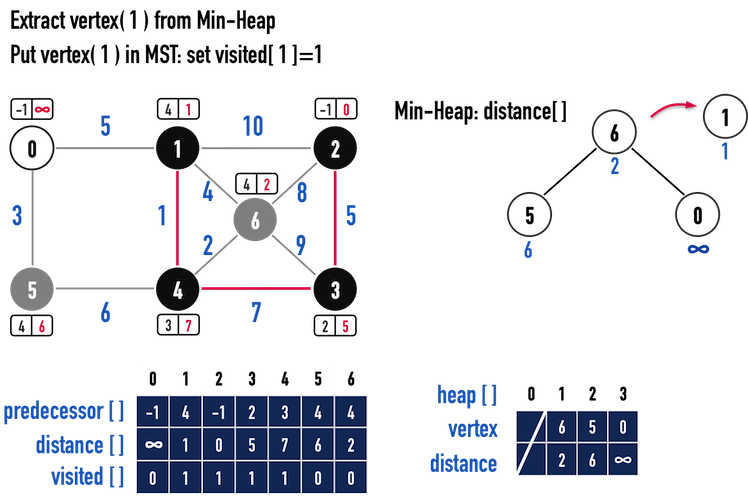
圖一(h)。
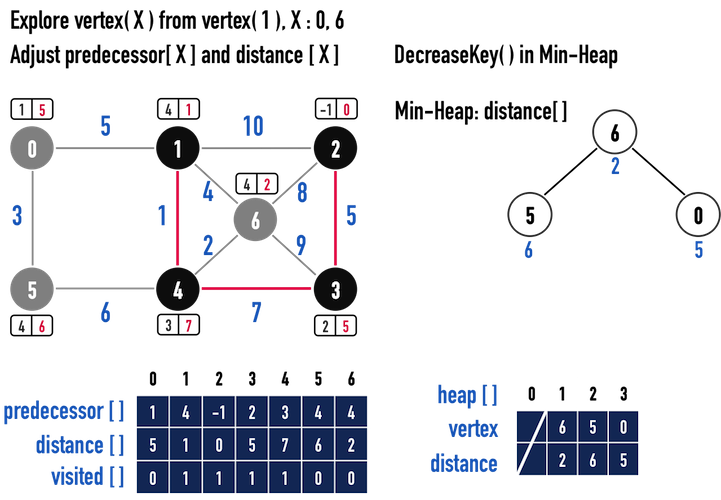
圖一(i)。
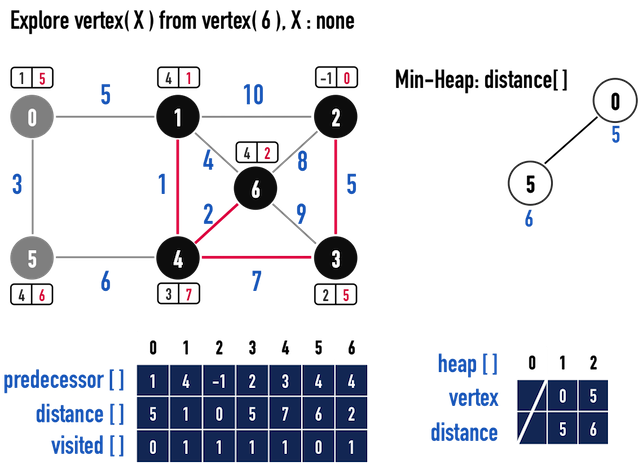
圖一(j)。
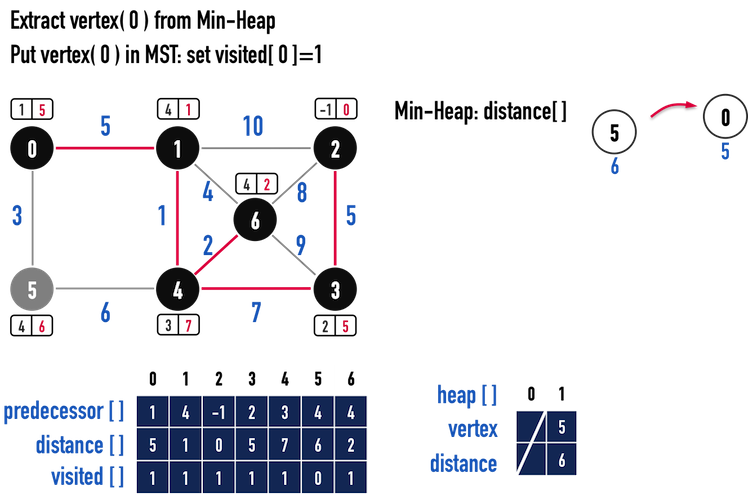
圖一(k)。
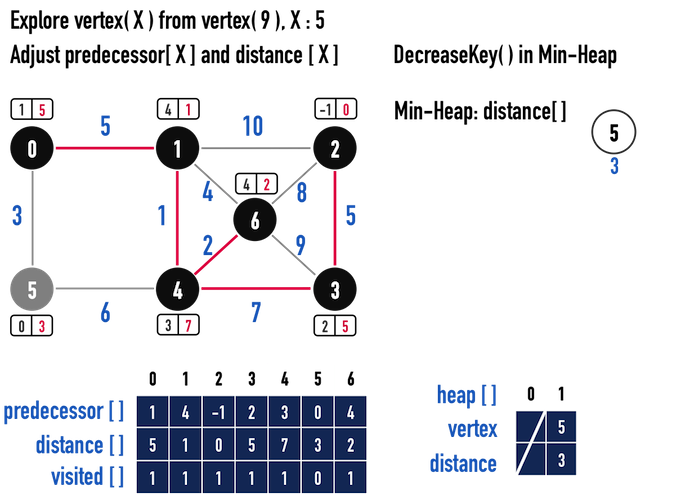
圖一(l)。
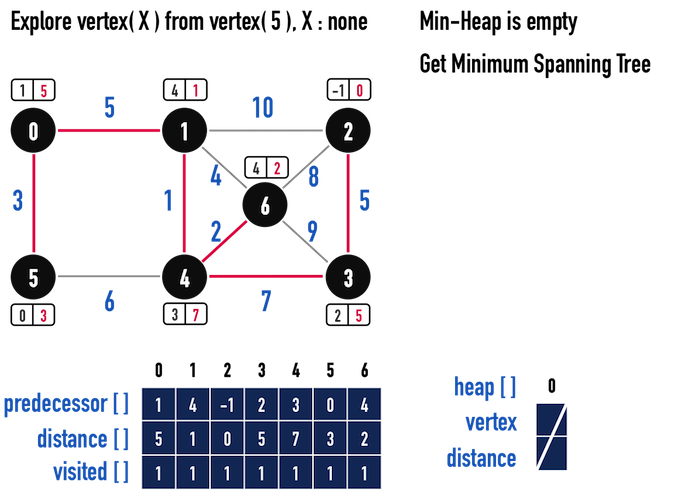
圖一(m)。
程式碼
以下的程式範例包含了class BinaryHeap、class Graph_MST與main()。
class BinaryHeap的概念與程式碼與Priority Queue:Binary Heap的內容相同。
class Graph_MST建立Graph,其中Prim_MinQueue()即為尋找MST的Prim's Algorithm之函式主體。
最後,main()利用AddEdge()建立出Graph的AdjList,並執行Prim_MinQueue()。
// C++ code
#include <iostream>
#include <vector>
#include <list>
#include <utility> // for std::pair<>
#include <iomanip> // for std::setw()
#include <cmath> // for std::floor
using std::cout;
using std::endl;
/////////////// MinHeap ////////////////
struct HeapNode{
int key, element;
HeapNode():key(0),element(0){};
HeapNode(int key, int element):key(key),element(element){};
};
class BinaryHeap{
private:
std::vector<HeapNode> heap;
void swap(struct HeapNode &p1, struct HeapNode &p2);
int FindPosition(int node);
int GetParentNode(int node){return std::floor(node/2);};
public:
BinaryHeap(){heap.resize(1);};
BinaryHeap(int n){
heap.resize(n + 1); // 主要存放vertex及其distance的vector
}
// Min-Priority Queue
void MinHeapify(int node, int length);
void BuildMinHeap(std::vector<int> array);
void DecreaseKey(int node, int newKey);
void MinHeapInsert(int node, int key);
int ExtractMin(); // 回傳heap[1]並調整Heap
int Minimum(){return heap[1].element;}; // 回傳heap[1]
bool IsHeapEmpty(){return (heap.size()<=1);};
};
int BinaryHeap::FindPosition(int node){
int idx = 0;
for (int i = 1; i < heap.size(); i++) {
if (heap[i].element == node) {
idx = i;
}
}
return idx;
}
void BinaryHeap::MinHeapInsert(int node, int key){
heap.push_back(HeapNode(node,key));
DecreaseKey(node, key);
}
void BinaryHeap::DecreaseKey(int node, int newKey){
int index_node = FindPosition(node); // 找到node所在的位置index
if (newKey >= heap[index_node].key) { // 如果不是把node的Key下修, 便終止此函式
std::cout << "new key is not smaller than current key\n";
return;
}
heap[index_node].key = newKey; // 更新node之Key後,
// 需要檢查是否新的subtree滿足Min Heap
while (index_node > 1 && heap[GetParentNode(index_node)].key > heap[index_node].key) {
swap(heap[index_node], heap[GetParentNode(index_node)]);
index_node = GetParentNode(index_node);
}
}
void BinaryHeap::swap(struct HeapNode &p1, struct HeapNode &p2){
struct HeapNode temp = p1;
p1 = p2;
p2 = temp;
}
int BinaryHeap::ExtractMin(){
if (IsHeapEmpty()) {
std::cout << "error: heap is empty\n";
exit(-1);
}
int min = heap[1].element; // 此時heap的第一個node具有最小key值
// 便以min記錄其element, 最後回傳min
// delete the first element/vertex
heap[1] = heap[heap.size()-1]; // 把最後一個element放到第一個位置,
heap.erase(heap.begin()+heap.size()-1); // 再刪除最後一個element
MinHeapify(1, (int)heap.size()); // 目前, heap[1]具有最大Key, 需要進行調整
return min; // 回傳heap中具有最小key的element
}
void BinaryHeap::BuildMinHeap(std::vector<int> array){
// 將array[]的資料放進 heap之矩陣中, 並預留 heap[0] 不做使用
for (int i = 0; i < array.size(); i++) {
heap[i + 1].element = i; // 把array[]的idx視為element
heap[i + 1].key = array[i]; // 把array[]的數值視為key
}
for (int i = (int)heap.size()/2; i >= 1 ; i--) {
MinHeapify(i, (int)heap.size()-1); // length要減一, 因為heap從從1開始存放資料
}
}
void BinaryHeap::MinHeapify(int node, int length){
int left = 2*node, // 取得left child
right = 2*node + 1, // 取得right child
smallest; // smallest用來記錄包含root與child, 三者之中Key最小的node
if (left <= length && heap[left].key < heap[node].key)
smallest = left;
else
smallest = node;
if (right <= length && heap[right].key < heap[smallest].key)
smallest = right;
if (smallest != node) { // 如果目前node的Key不是三者中的最小
swap(heap[smallest], heap[node]); // 就調換node與三者中Key最小的node之位置
MinHeapify(smallest, length); // 調整新的subtree成Min Heap
}
}
/////////////// Prim's Algorithm /////////////////
static const int maxDistance = 100;
class Graph_MST{
private:
int num_vertex;
std::vector<std::list<std::pair<int,int> > > AdjList;
std::vector<int> predecessor, distance;
std::vector<bool> visited;
void InitializeSingleSource(int Start); // 以Start作為起點
void PrintDataArray(std::vector<int> array);
public:
Graph_MST():num_vertex(0){};
Graph_MST(int n):num_vertex(n){
AdjList.resize(num_vertex);
}
void AddEdge(int from, int to, int weight);
void Prim_MinQueue(int Start);
friend class BinaryHeap;
};
void Graph_MST::InitializeSingleSource(int Start){
distance.resize(num_vertex);
predecessor.resize(num_vertex);
for (int i = 0; i < num_vertex; i++) {
distance[i] = maxDistance;
predecessor[i] = -1;
}
distance[Start] = 0; // 起點vertex的distance設為0, ExtractMin就會從起點開始
}
void Graph_MST::Prim_MinQueue(int Start){
InitializeSingleSource(Start);
BinaryHeap minQueue(num_vertex);
minQueue.BuildMinHeap(distance); // use minQueue to handle distance[]
visited.resize(num_vertex, false); // initializa visited[] as {0,0,0,...,0}
while (!minQueue.IsHeapEmpty()) {
int u = minQueue.ExtractMin();
visited[u] = true;
for (std::list<std::pair<int, int> >::iterator itr = AdjList[u].begin();
itr != AdjList[u].end(); itr++) {
if (visited[(*itr).first] == false && (*itr).second < distance[(*itr).first]) {
// for edge(X,Y)
// u: X , (*itr).first: Y, (*itr).second: weight(X,Y)
// (*itr).second < distance[(*itr).first]: weight(X,Y) < distance[Y]
distance[(*itr).first] = (*itr).second;
predecessor[(*itr).first] = u;
minQueue.DecreaseKey((*itr).first, distance[(*itr).first]);
}
}
}
/////// print result /////////
cout << "print predecessor[]:\n";
PrintDataArray(predecessor);
cout << "print distance[]:\n";
PrintDataArray(distance);
cout << std::setw(3) << "v1" << " - " << std::setw(3) << "v2"<< " : weight\n";
int i = (Start+1)%num_vertex; // 若從4開始, i依序為5,6,0,1,2,3
while (i != Start) {
cout << std::setw(3) << predecessor[i] << " - " << std::setw(3) << i
<< " : " << std::setw(3) << distance[i] <<"\n";
i = (++i)%num_vertex; // 到了6之後, 6+1 = 7, error:bad_access
}
}
void Graph_MST::PrintDataArray(std::vector<int> array){
for (int i = 0; i < num_vertex; i++){
cout << std::setw(4) << i;
}
std::cout << endl;
for (int i = 0; i < num_vertex; i++){
cout << std::setw(4) << array[i];
}
cout << endl << endl;
}
void Graph_MST::AddEdge(int from, int to, int weight){
AdjList[from].push_back(std::make_pair(to,weight));
}
int main(){
Graph_MST g6(7);
g6.AddEdge(0, 1, 5);g6.AddEdge(0, 5, 3);
g6.AddEdge(1, 0, 5);g6.AddEdge(1, 2, 10);g6.AddEdge(1, 4, 1);g6.AddEdge(1, 6, 4);
g6.AddEdge(2, 1, 10);g6.AddEdge(2, 3, 5);g6.AddEdge(2, 6, 8);
g6.AddEdge(3, 2, 5);g6.AddEdge(3, 4, 7);g6.AddEdge(3, 6, 9);
g6.AddEdge(4, 1, 1);g6.AddEdge(4, 3, 7);g6.AddEdge(4, 5, 6);g6.AddEdge(4, 6, 2);
g6.AddEdge(5, 0, 3);g6.AddEdge(5, 4, 6);
g6.AddEdge(6, 1, 4);g6.AddEdge(6, 2, 8);g6.AddEdge(6, 3, 9);g6.AddEdge(6, 4, 2);
cout << "MST found by Prim_MinQueue:\n";
g6.Prim_MinQueue(2);
return 0;
}
output:
MST found by Prim_MinQueue:
print predecessor:
0 1 2 3 4 5 6
1 4 -1 2 3 0 4
print distance:
0 1 2 3 4 5 6
5 1 0 5 7 3 2
v1 - v2 : weight
2 - 3 : 5
3 - 4 : 7
0 - 5 : 3
4 - 6 : 2
1 - 0 : 5
4 - 1 : 1
結果如同圖一(m):

圖一(m)。
以上便是利用Min-Priority Queue實作的Prim's Algorithm之介紹。
建議讀者可以稍微比較一下以下兩者:
- 利用Min-Priority Queue實作的Prim's Algorithm,以及
- 利用Min-Priority Queue實作的Dijkstra's Algorithm。
根本一模一樣。
參考資料:
- Introduction to Algorithms, Ch23
- Fundamentals of Data Structures in C++, Ch6
- Rashid Bin Muhammad:Jarnik's (Prim's) Algorithm
- Theory of Programming:Prim's Algorithm
- GeeksforGeeks:Greedy Algorithms | Set 6 (Prim’s MST for Adjacency List Representation)
- Single-Source Shortest Path:Dijkstra's Algorithm
- Priority Queue:Binary Heap
MST系列文章
Minimum Spanning Tree:Intro(簡介)
Minimum Spanning Tree:Kruskal's Algorithm
Minimum Spanning Tree:Prim's Algorithm
Minimum Spanning Tree:Prim's Algorithm using Min-Priority Queue
回到目錄: