Priority Queue：Binary Heap

先備知識與注意事項

本篇文章將接續Priority Queue：Intro(簡介)，介紹Binary Heap(二元堆積)，並用以實現Min-Priority Queue。

Binary Heap的概念與Binary Tree密切相關，若讀者有興趣，不妨回顧一下何謂Complete Binary Tree暖暖身，請參考：Binary Tree: Intro(簡介)。

目錄

• Binary Heap(二元堆積)
• Binary Heap之Operation(函式)
  • 函式：MinHeapify
  • 函式：BuildMinHeap
  • 函式：其他
  • 函式：Minimum
  • 函式：ExtractMin
  • 函式：DecreaseKey
  • 函式：MinHeapInsert
• 參考資料
• Priority Queue系列文章

Binary Heap(二元堆積)

為處理廣義情形，建議將Binary Heap中的元素定義為Dictionary，每個資料項目皆有其對應的Key值，也就是Priority Queue將使用的Key。
(關於Dictionary，請參考：Hash Table：Intro(簡介)以及Binary Search Tree: Intro(簡介))

Binary Heap有兩項基本特徵：

特徵一：Binary Heap之結構可以視作Complete Binary Tree。

• 如圖一(a)，A\(\sim\)I共9個元素，便按照Complete Binary Tree之順序規則，填滿位置\(1\sim9\)，以index(\(1\))\(\sim\)index(\(9\))表示。

這樣的優點是易於尋找「parent-child」之關係，以index(\(i\))的node為例：

• 其left child必定位在index(\(2i\))；
• 其right child必定位在index(\(2i+1\))；
• 其parent必定位在index(\(\lfloor i/2 \rfloor\))。

以圖一(a)中位於index(\(3\))之node(F)為例：

• 其left child為index(\(6\))之node(E)；
• 其right child為index(\(7\))之node(I)；
• 其parent為index(\(1\))之node(D)。

圖一(a)。

特徵二，若將位於index(\(i\))之node視為subtree之root，那麼，可將此Binary Heap分為兩類：

• Max Heap：在每一個subtree中，root之「key」要比兩個child之「key」還要大：
  • \(Key(i)>Key(2i)\)
  • \(Key(i)>Key(2i+1)\)
• Min Heap：在每一個subtree中，root之「key」要比兩個child之「key」還要小：
  • \(Key(i)<Key(2i)\)
  • \(Key(i)<Key(2i+1)\)

以圖一(b)之Min Heap為例，每個node下方的藍色數字表示其Key值，檢查Min-Heap中任何一個subtree，皆滿足\(Key(i)<Key(2i)\)以及\(Key(i)<Key(2i+1)\)。

圖一(b)。

由於Binary Heap特有的「parent-child」之關係，只要讓矩陣中index(\(0\))的位置閒置，從index(\(1\))開始存放資料之Dictionary，便能夠使用矩陣(array)來表示Binary Heap，如圖一(b)。

Binary Heap中的每個資料(node)之Dictionary將以struct實現：
(亦可使用std::pair<int,int>或其他)

// C++ code
struct HeapNode{
    int element, key;
    HeapNode():element(0),key(0){};
    HeapNode(int node, int key):element(node), key(key){};
};

備註：為了區別element與key，圖示中的element是以「英文字母」表示，而key用int。不過這裡定義的struct HeapNode之element是以int表示，主要是為了使這篇文章定義的Min-Priority Queue可以在Minimum Spanning Tree：Prim's Algorithm using Min-Priority Queue與Single-Source Shortest Path：Dijkstra's Algorithm直接複製貼上使用。

class BinaryHeap之定義，以及所有成員函式(member function)之宣告如下：

// C++ code
class BinaryHeap{
private:
    std::vector<HeapNode> heap;        // 存放HeapNode資料的矩陣
    void swap(struct HeapNode &p1, struct HeapNode &p2);
    int FindPosition(int node);
    int GetParentNode(int node){return std::floor(node/2);};
public:
    BinaryHeap(){               // default constructor會把heap[0]給預留 
        heap.resize(1);         // 之後若新增HeapNode, 會從heap[1]開始新增
    }
    BinaryHeap(int n){
        heap.resize(n + 1);
    }
    bool IsHeapEmpty(){return (heap.size()<1);};

    // Min-Priority Queue
    void MinHeapify(int node, int length);
    void BuildMinHeap(std::vector<int> array);
    void DecreaseKey(int node, int newKey);
    void MinHeapInsert(int node, int key);
    int Minimum();                  // 回傳vertex的位置index
    int ExtractMin();               // 回傳vertex的位置index

    // void HeapSort();

    // Max-Priority Queue
    ...
};

Binary Heap之Operation(函式)

接著要介紹和Min Heap與Min-Priority Queue有關的函式。

小小提醒：為避免混淆，在圖示介紹中，資料的「element」是以「英文字母」表示，而實際的程式碼，資料的「element」仍是用int，例如，使用\(A-1\)、\(B-2\)做對應。

函式：MinHeapify

MinHeapify()是一種「由上至下」(由root往leaf)，按照Min Heap之規則逐一調整subtree的方法，步驟如下：

• 選定某個index(\(i\))之node(\(i\))，視為subtree之root；
• 比較root的Key與兩個child(node(\(2i\))與node(\(2i+1\)))之Key；
  • 如果left child之Key最小，則將node(\(i\))與node(\(2i\))對調位置，使原先的left child成為root；
  • 如果right child之Key最小，則將node(\(i\))與node(\(2i+1\))對調位置，使原先的right child成為root；
• 並在對調之後，繼續檢查「新的subtree」是否滿足Min Heap的規則。

以圖二(a)為例，node(K)、node(Y)、node(Z)所形成的subtree不符合Min Heap的規則，因此：

• 比較三者的Key，以變數int smallest記錄具有最小Key值的node。
• smallest是Key為\(17\)的node(Y)，則將node(K)與node(Y)互換位置，如圖二(b)。

圖二(a)。

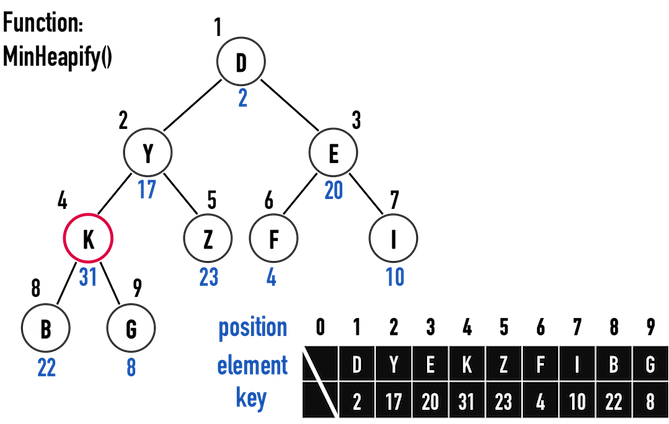
圖二(b)。

在經過以上步驟之後，node(K)、node(Y)、node(Z)所形成的subtree已經滿足Min Heap的規則。

不過，由於node(K)之Key值比node(Y)之Key值大，因此，即使原先由node(Y)、node(B)、node(G)形成之subtree滿足Min Heap規則(以圖二(a)的情形為例，原先已經不滿足Min Heap)，仍不能保證node(K)取代node(Y)後，node(K)、node(B)、node(G)所形成之subtree也滿足Min Heap規則，所以需要重複上述步驟，再次以node(K)作為subtree之root，檢查並調整subtree成Min Heap，如圖二(c)與圖二(d)。

圖二(c)。

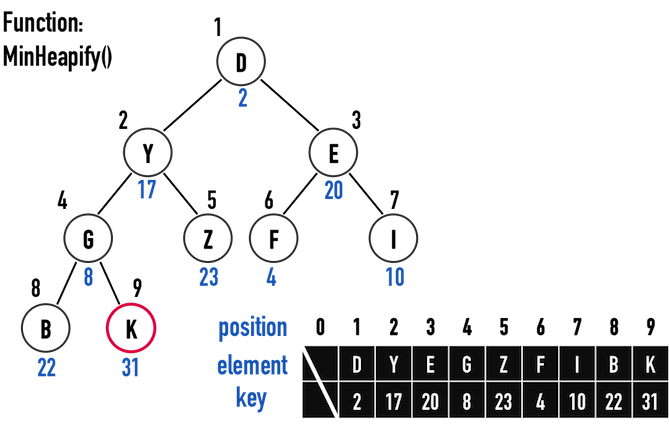
圖二(d)。

因為smallest挑的是node(\(i\))、node(\(2i\))、node(\(2i+1\))中Key值最小的node，使之成為subtree之root，因此「所有被檢查過的」subtree，必定滿足Min Heap之規則，如圖二(d)中的「node(Y)、node(G)、node(Z)」與「node(G)、node(B)、node(K)」。

但是，Binary Heap中仍然可能有某些subtree不符合Min Heap規則，如圖二(d)中的「node(E)、node(F)、node(I)」，因此，會需要一個迴圈對「所有具有child的node」進行檢查(利用MinHeapify()檢查)，這就是下一個函式BuildMinHeap()的任務。

MinHeapify()之範例程式碼如下：

// C++ code
void BinaryHeap::MinHeapify(int node, int length){

    int left = 2*node,          // 取得left child
        right = 2*node + 1,     // 取得right child
        smallest;               // smallest用來記錄包含root與child, 三者之中Key最小的node

    if (left <= length && heap[left].key < heap[node].key)
        smallest = left;
    else
        smallest = node;

    if (right <= length && heap[right].key < heap[smallest].key)
        smallest = right;

    if (smallest != node) {                 // 如果目前node的Key不是三者中的最小
        swap(heap[smallest], heap[node]);   // 就調換node與三者中Key最小的node之位置
        MinHeapify(smallest, length);       // 調整新的subtree成Min Heap
    }
}

函式：BuildMinHeap

BuildMinHeap()的任務很簡單，把每一個「具有child」的node都進行過一次MinHeapify()，如此便能保證Binary Heap中的所有subtree皆滿足Min Heap規則，便能將一個由任意矩陣代表的Binary Heap轉換成Min Heap。

根據Binary Heap的index(\(i\))特徵：

• left child在index(\(2i\))；
• right child在index(\(2i+1\))；
• parent在index(\(\lfloor i/2 \rfloor\))；

若Binary Heap共有\(N\)個node，那麼所有「具有child」的node，必定位在index(\(i\))到index(\(\lfloor N/2 \rfloor\))。

以圖三(a)中的任意Binary Heap(還不是Min Heap)為例，共有\(9\)個node，因此，必定只有index(\(1\))到index(\(4\))的node具有child。

圖三(a)。

因此，BuildMinHeap()只要從index(\(4\))之node，一路往index(\(1\))之node進行MinHeapify()，便能將此Binary Heap轉換成Min Heap，見圖三(b)。

圖三(b)。

BuildMinHeap()之範例程式碼如下：

• input：給定一個任意矩陣array[]。

  • 此處給定std::vector<int> array，把array的index視為element，把array的數值視為key。

    • 若array[] = {\(100,27,34,56,...\)}，那麼key(\(100\))就對應到element(\(0\))，key(\(27\))對應到element(\(1\))，key(\(34\))對應到element(\(2\))，依此類推。
    • 例如在Graph問題中，array的index時常對應到「特定的vertex」，例如BFS()的distance[]，distance[1]即表示「從起點vertex走到vertex(1)」的距離，因此不需要特別使用struct HeapNode表示array的矩陣元素。

  • 也可以把input令成std::vector<HeapNode> array，那麼每一個矩陣元素都有各自的element與key，依序放進std::vector<HeapNode> heap即可。

• heap[]初始化：先把array[]的資料放進heap[]，並將heap[0]閒置。

• 接著對index(\(\lfloor N/2 \rfloor\))到index(\(1\))進行MinHeapify()。
  
  

// C++ code
void BinaryHeap::BuildMinHeap(std::vector<int> array){

    // 將array[]的資料放進 heap之矩陣中, 並預留 heap[0] 不做使用
    for (int i = 0; i < array.size(); i++) {     
        heap[i + 1].element = i;                 // 把array[]的idx視為element
        heap[i + 1].key = array[i];              // 把array[]的數值視為key
    }
    for (int i = (int)heap.size()/2; i >= 1 ; i--) {
        MinHeapify(i, (int)heap.size()-1);     // length要減一, 因為heap從從1開始存放資料
    }
}

函式：其他

在進入與Min-Priority Queue有關的函式之前，先介紹些其他(雜項)放鬆心情。

首先是在MinHeapify()出現過的swap()，單純地利用reference作為函式的參數，對Heap中的node進行位置調換：

// C++ code
void BinaryHeap::swap(struct HeapNode &p1, struct HeapNode &p2){

    struct HeapNode temp = p1;
    p1 = p2;
    p2 = temp;
}

FindPosition()是為了確認特定元素所在的位置(index)，這會用在Min-Priority Queue中的DecreaseKey()，因為其需要先「找到資料在Heap中的位置」，再調整該資料之Key。

不過由於DecreaseKey()的時間複雜度只有\(O(\log N)\)，若使用以下的直覺寫法，缺點是會把時間複雜度提高到\(O(N)\)(其中\(N\)為node總數)。
還有一些替代方法，例如以空間換取時間，設立一個矩陣變數，記錄每一筆資料的位置，便能維持DecreaseKey()的效率。

這部分就留給讀者自行斟酌。

// C++ code
int BinaryHeap::FindPosition(int node){

    int idx = 0;
    for (int i = 1; i < heap.size(); i++) {
        if (heap[i].element == node) {
            idx = i;
        }
    }
    return idx;
}

以及定義在class BinaryHeap裡面的IsHeapEmpty()與GetParentNode()，分別檢查Heap是否有資料，和回傳node(i)之parent的index(\(\lfloor i/2 \rfloor\))：

// C++ code
class BinaryHeap{
    ...
    bool IsHeapEmpty(){return (heap.size()<1);};
    int GetParentNode(int node){return std::floor(node/2);};
    ...
};

函式：Minimum

因為Min Queue的規則，root一定是所有node中，具有最小Key值的node，因此，若要得到最小值，只要讀取heap[1]即可：

// C++ code
int BinaryHeap::Minimum(){
    return heap[1].element;
}

函式：ExtractMin

ExtractMin()的目的是「回傳具有最小Key的node之index」，並且將其從Heap中移除，步驟如下：

• 確認Heap是否有資料，若沒有的話，便回傳error：巧婦難為無米之炊。
• 若Heap中有資料，先以變數min記下Min Heap中的root之element，root即為Heap中具有最小Key值之node；
• 接著把Heap中「最後一個node」之資料放進「第一個index位置」裡面，如此便從Heap中移除原先的「最小Key值node」；

• 由於在上個步驟已經把原先位於「最後位置index」之node放進root之位置，便能夠直接刪除最後一個位置的記憶體位置，調整存放資料的heap；

  • 在此，因為使用了C++標準函式庫(STL)的std::vector，若要刪除heap的最後一個元素，只要只用成員函式(member function)：std::vector::erase()即可。
    (關於std::vector::erase，請參考：Cplusplus：std::vector::erase)

• 此時，root位置的node之Key極有可能比其兩個child之Key值還要大，有可能違反Min Heap規則，因此需要對其執行MinHeapify()。

以圖四(a)為例，要取出Min Heap的root，也就是Key值為2的node(D)，並且將Min Heap中，位在最後一個index之node(C)放進root，然後利用MinHeapify()重新將Heap調整成Min heap，如圖四(b)。

圖四(a)。

圖四(b)。

ExtractMin()之範例程式碼如下：

// C++ code
int BinaryHeap::ExtractMin(){

    if (IsHeapEmpty()) {
        std::cout << "error: heap is empty\n";
        exit(-1);
    }
    int min = heap[1].element;    // 此時heap的第一個node具有最小key值
                                  // 便以min記錄其element, 最後回傳min
    // delete the first element/vertex
    heap[1] = heap[heap.size()-1];            // 把最後一個element放到第一個位置,
    heap.erase(heap.begin()+heap.size()-1);   // 再刪除最後一個element
    MinHeapify(1, (int)heap.size());          // 目前, heap[1]具有最大Key, 需要進行調整

    return min;       // 回傳heap中具有最小key的element
}

函式：DecreaseKey

DecreaseKey()的目的是調整Min Heap中的node之Key值，因為Key值改變，極有可能違反Min Heap規則，因此也需要對Heap進行調整，步驟如下：

• 由於函式的參數(argument)是struct結構中的element，若以圖五(a)為例，資料的element就是「英文字母」(A、B、C等等)，因此，先利用FindPosition()找到該資料在Heap中的位置index；
• 再判斷，若參數中的newKey沒有比原先的Key還小，就直接結束函式(可以想成DecreaseKey()只有把資料之Key降低，沒有調高的功能)；
• 若沒有在上個步驟結束函式，便把資料之Key更新成newKey；
  • 因為使用矩陣存放資料，所以只要有資料在Heap中的index，即可靠index對資料進行存取。
• 因為是把資料的Key「降低」，因此，有可能使得原先資料所位於的subtree違反Min Heap規則，需要調整：
  • 假設被修改的資料是位於index(\(i\))的node(\(i\))，便比較node(\(i\))與其parent(也就是node(\(\lfloor i/2 \rfloor\)))之Key值，
  • 如果node(\(i\))之Key值較小，便交換index(\(i\))與index(\(\lfloor i/2 \rfloor\))的資料(如同在Minheapify()中的交換swap())。
  • 若node(\(i\))之Key值仍然比其parent之Key值大，表示，node(\(i\))所在之subtree仍滿足Min Heap規則，即可結束函式。
  • 還有，由於Heap的root是從index(\(1\))開始存放資料，若一路回溯parent直到index小於\(1\)，表示Heap中所有與「被修改的資料」有關之subtree都被檢查過了，可以結束函式。

圖五(a)。

以圖五(a)為例，若將node(H)之Key值從原先的\(15\)更改成\(3\)，將使得subtree「node(A)、node(G)、node(H)」違反Min Heap規則，如圖五(b)，必須利用上述方法修正。
修正流程見圖五(c)。

圖五(b)。

圖五(c)。

DecreaseKey()之範例程式碼如下：
(函式裡的int node與struct HeapNode的element具有相同意義)

// C++ code
void BinaryHeap::DecreaseKey(int node, int newKey){

    int index_node = FindPosition(node);      // 找到node所在的位置index

    if (newKey > heap[index_node].key) {      // 如果不是把node的Key下修, 便終止此函式
        std::cout << "new key is larger than current key\n";
        return;
    }
    heap[index_node].key = newKey;            // 更新node之Key後, 需要檢查是否新的subtree滿足Min Heap
    while (index_node > 1 && heap[GetParentNode(index_node)].key > heap[index_node].key) {
        swap(heap[index_node], heap[GetParentNode(index_node)]);
        index_node = GetParentNode(index_node);
    }
}

函式：MinHeapInsert

有了DecreaseKey()後，要在Min Heap中新增資料會容易許多：
(若恰好以std::vector建立heap[]，簡直只要兩行程式碼)

• 在Heap中多配置一塊新的記憶體位置，也就是把用來儲存Heap之矩陣heap[]拉長，存放新的資料；
• 現在新的資料已經位於Heap中的最後一個位置index，只要利用DecreaseKey()，即可將新的Heap調整成Min Heap。
  • 因為DecreaseKey()並不會阻止「newKey等於node現有Key」的情形，所以，即使在DecreaseKey()的輸入參數(input argument)上，newKey若等於已經存在Heap中的node之Key也是可行的。

以圖六(a)為例，若要在Heap中新增Key為\(6\)之node(J)，便將其加入heap[]的最後位置，再利用DecreaseKey()比較node(J)與其parent之Key值，檢查是否符合Min Heap規則，若不符合即進行修正，見圖六(a)-圖六(c)。

圖六(a)。

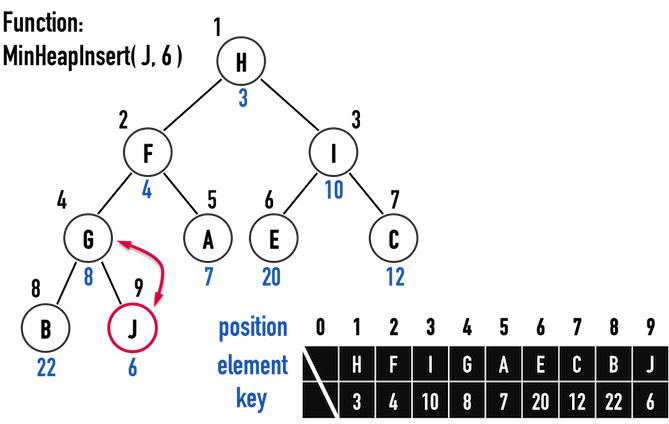
圖六(b)。

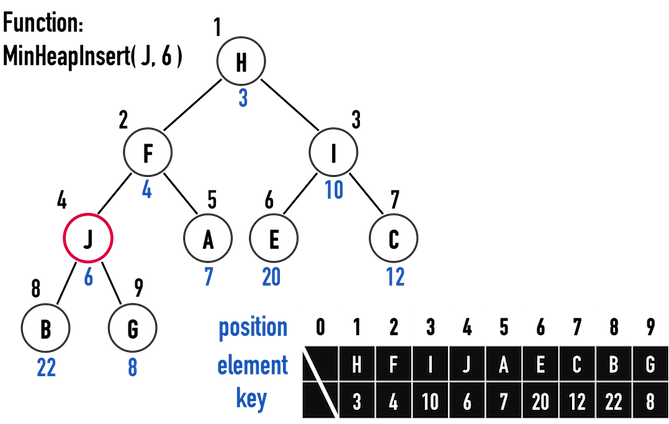
圖六(c)。

MinHeapInsert()之範例程式碼如下：
(函式裡的int node與struct HeapNode的element具有相同意義)

// C++ code
void BinaryHeap::MinHeapInsert(int node, int key){

    heap.push_back(HeapNode(node,key));    // 在heap[]尾巴新增一個node
    DecreaseKey(node, key);
}

由以上說明可以發現，在MinHeapify()中，是「由上往下」對subtree進行修正，有的寫法會將此操作獨立成函式：SiftDown；
在DecreaseKey()中，則是「由下往上」進行修正，此則稱為SiftUp，範例請參考：Code Review：Implementation of binary heap in C++。

以上便是以Binary Heap實現Min-Priority Queue之說明，後者將在許多應用出現，包括與Graph相關的Prim's Algorithm和Dijkstra's Algorithm。

參考資料：

• Introduction to Algorithms, Ch6
• Fundamentals of Data Structures in C++, Ch5, Ch9
• Ashley Montanaro：Priority queues and Dijkstra’s algorithm
• 禪心劍氣相思骨：Priority Queue 解析1 - 從binary heap開始
• Binary Tree: Intro(簡介)
• Code Review：Implementation of binary heap in C++
• Single-Source Shortest Path：Dijkstra's Algorithm
• Minimum Spanning Tree：Prim's Algorithm using Min-Priority Queue
• Wikipedia：Priority Queue
• Wikipedia：Binary Heap

Priority Queue系列文章

Priority Queue：Intro(簡介)
Priority Queue：Binary Heap

回到目錄：

目錄：演算法與資料結構