Flow Networks：Maximum Flow & Ford-Fulkerson Algorithm

先備知識與注意事項

考慮如下情境：

在某個污水處理廠的某一道程序裡，有一個「進水孔」，和一個「排水孔」，中間由許多「孔徑不一」的水管連接起來，因為水管的「孔徑大小」會影響到「每單位時間的流量」，因此要解決的問題，就是找到每單位時間可以排放「最大流量(flow)」的「排水方法」。

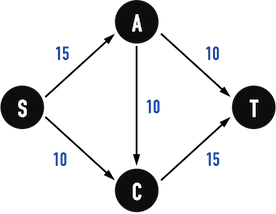
圖一。

以圖一為例，進水孔為vertex(S)，排水孔為vertex(T)，中間要經過污水處理站vertex(A)與vertex(C)。
edge代表水管，edge之weight(以下將稱為capacity)表示水管的「孔徑」。

考慮兩種「排水方法」的flow：

1. 第一種「分配水流」的方法，每單位時間總流量為\(20\)：
   1. 在\(Path:S-A-T\)上每單位時間流了\(5\)單位的水；
   2. 在\(Path:S-A-C-T\)上每單位時間流了\(10\)單位的水(問題出在這，占去了edge(C,T)的容量)；
   3. 在\(Path:S-C-T\)上，因為edge(C,T)上只剩下「\(5\)單位的容量」，因此每單位時間流了\(5\)單位的水；
2. 第二種「分配水流」的方法，每單位時間總流量為\(25\)：
   1. 在\(Path:S-A-T\)上每單位時間流了\(10\)單位的水；
   2. 在\(Path:S-A-C-T\)上每單位時間流了\(5\)單位的水；
   3. 在\(Path:S-C-T\)上，因為edge(C,T)上剛好還有「\(10\)單位的容量」，因此每單位時間流了\(10\)單位的水；

從以上兩種「排水方式」可以看得出來，解決問題的精神，就是如何有效利用水管的「孔徑容量」，讓最多的水可以從「進水孔」流到「排水孔」。

這就是在Flow Networks上找到Maximum Flow(最大流量)的問題。

以下將介紹Ford-Fulkerson Algorithm(若使用BFS搜尋路徑，又稱為Edmonds-Karp Algorithm)來回應此問題。

目錄

• Flow Networks基本性質
• Ford-Fulkerson Algorithm
  • Residual Networks(剩餘網路)
  • Augmenting Paths(增廣路徑)
  • 演算法概念
• 程式碼
• 利用BFS的優點
• 參考資料
• Flow Networks系列文章

Flow Networks基本性質

Flow Networks是一個weighted,directed graph，其edge(X,Y)具有非負的capacity，\(c(X,Y)\geq 0\)，如圖二(a)。
(此處以capacity取代weight，capacity就是「水管孔徑」。)

• 若不存在edge(X,Y)，則定義\(c(X,Y)=0\)。
• 特別區分兩個vertex：
  • source：表示Flow Networks的「流量源頭」，以s表示；
  • sink：表示Flow Networks的「流量終點」，也稱為termination，以t表示。

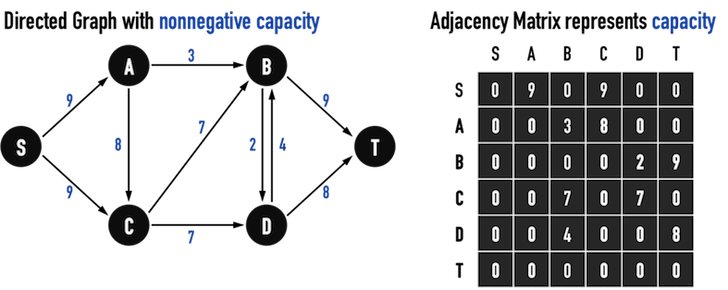
圖二(a)。

而水管裡的「水流」，flow，必須滿足以下條件，見圖二(b)：

1. Capacity constraint：從vertex(X)流向vertex(Y)的flow，不能比edge(X,Y)的capacity還大，\(f(X,Y)\leq c(X,Y)\)。
   • 若每單位時間內，水管孔徑只能容納\(5\)單位，那flow最多就是\(5\)單位。
   • 以圖二(b)為例，在\(Path:S-A-C-D-T\)上的edge之capacity皆大於\(6\)，因此在此路徑上流入\(6\)單位的flow是可行的。
2. Skew symmetry：若定義「從vertex(X)指向vertex(Y)」之edge(X,Y)上，有\(5\)單位的flow，\(f(X,Y)=5\)，這就等價於，從vertex(Y)到vertex(X)之edge(Y,X)上，有\(-5\)單位的flow，\(f(Y,X)=-5\)。
   • 與「電子流(負電荷)」與「電流(正電荷)」之概念雷同，從「左到右的電流」與「從右到左的電子流」具有等價的物理意義。
3. Flow conservation：對Graph中除了source與sink以外的vertex(X)而言，所有「流進flow」之總和要等於所有「流出flow」的總和。
   • 也就是水流不會無故增加或無故減少，可視為一種能量守恆。
   • 以圖二(b)為例，流入vertex(A)的flow為\(6\)，流出vertex(A)的flow也是\(6\)，對vertex(C)、vertex(D)也是。

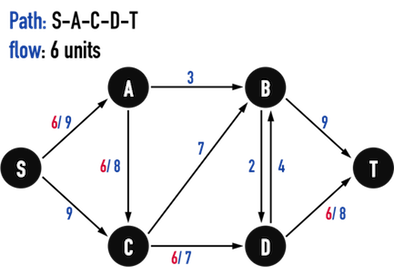
圖二(b)。

Ford-Fulkerson Algorithm

Ford-Fulkerson Algorithm需要兩個輔助工具：

1. Residual Networks(剩餘網路)
2. Augmenting Paths(增廣路徑)

Residual Networks(剩餘網路)

Residual Networks的概念為，記錄Graph上之edge還有多少「剩餘的容量」可以讓flow流過。

以圖三(a)為例，若在\(Path:S-A-C-D-T\)上的所有edge都有\(6\)單位的flow流過，那麼這些edge(edge(S,A)、edge(A,C)、edge(C,D)、edge(D,T))的可用「剩餘capacity」，都應該要「減\(6\)」，例如，edge(S,A)只能「再容納\(9-6=3\)單位」的flow，edge(C,D)只能「再容納\(7-6=1\)單位」的flow。

這些「剩餘capacity」就稱為residual capacity，以\(c_f\)表示。
若edge(X,Y)上有flow流過，\(f(X,Y)\)，便將edge(X,Y)上的residual capacity定義為：

• \(c_f(X,Y)=c(X,Y)-f(X,Y)\)
  • \(c(X,Y)\)為原來水管孔徑大小；
  • \(f(X,Y)\)表示目前水管已經有多少流量；
  • \(c_f(X,Y)\)表示水管還能再容納多少流量。

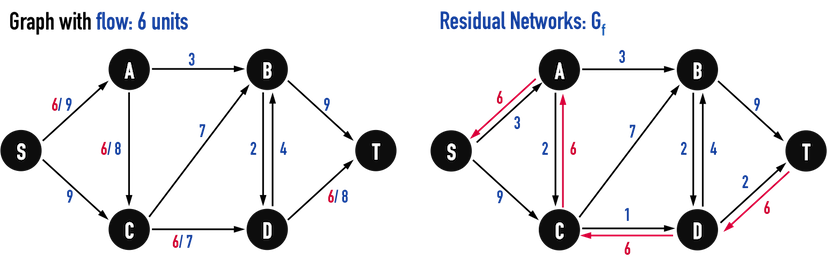
圖三(a)。

Residual Networks也是一個directed graph，其中：

• vertex集合與原directed graph完全相同；
• edge之capacity以residual capacity取代，見圖三(a)右。

最關鍵的是，若「從vertex(A)指向vertex(C)」之edge(A,C)上，有\(6\)單位的flow流過，\(f(A,C)=6\)，那麼在其Residual Networks上，會因應產生出一條「從vertex(C)指向vertex(A)」的edge(C,A)，並具有\(6\)單位的residual capacity，\(c_f(C,A)=6\)。

• 因為Skew symmetry，\(f(C,A)=-f(A,C)\)；
• 再根據定義，\(c_f(C,A)=c(C,A)-f(C,A)=c(C,A)+f(A,C)=0+6=6\)，

其物理意義呢？可以用「如果想要重新配置水流方向」來理解。

舉例來說，如果現在想經過\(Path:S-C-A-B-T\)流過\(2\)單位的flow，若觀察最一開始「還沒有flow經過」的directed graph(圖二(a))，其實並不存在從vertex(C)指向vertex(A)的edge(C,A)，因此\(c(C,A)=0\)，但是因為在圖三(a)已經有\(6\)單位的flow從vertex(A)流向vertex(C)，使得現在可以從edge(A,C)上把\(2\)單位的flow「收回」，轉而分配到edge(A,B)上，而edge(A,C)上，就剩下\(4\)單位的flow，最後的結果如圖三(b)左所示。
在新增一條「增加flow的Path」後，Residual Networks更新如圖三(b)右。

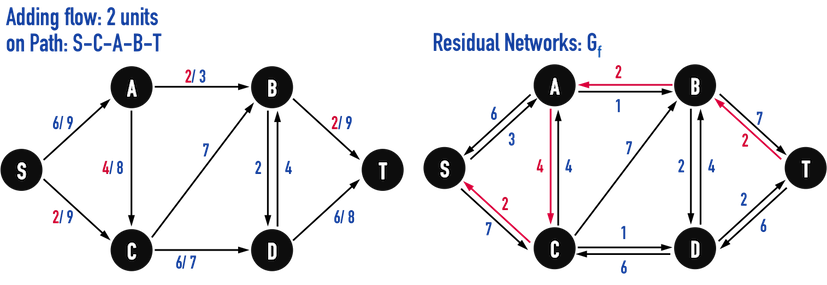
圖三(b)。

經過圖三(a)以及圖三(b)之後，流入sink(或稱termination)的flow累加到\(8\)單位。

Augmenting Paths(增廣路徑)

在Residual Networks裡，所有能夠「從source走到termination」的路徑，也就是所有能夠「增加flow的path」，就稱為Augmenting Paths。

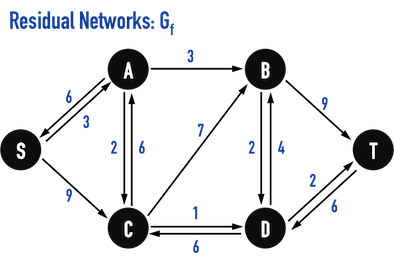
圖四(a)。

若以圖四(a)的Residual Networks為例，見圖四(b)，Augmenting Paths有許多可能，例如：

• \(Path:S-A-B-T\)，\(3\)單位的flow。
  • 因為在路徑上，所有edge中最小的capacity為\(c(A,B)=3\)，因此，flow可以容許從\(1\)單位到\(3\)單位。
• \(Path:S-C-B-D-T\)，\(2\)單位的flow。
  • 同理，因為在路徑上，所有edge中最小的capacity為\(c(B,D)=c(D,T)=2\)，因此，flow可以容許\(1\)單位或\(2\)單位。
• 以及其他。

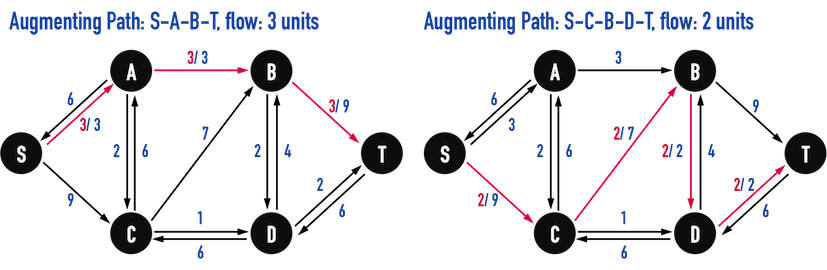
圖四(b)。

綜合以上可以確定，以圖四(c)為例：

• 若要看當前流入termination的「總流量」，要在圖四(c)左，edge上標示「flow/capacity」的Graph上找。
  • 如圖四(c)，流入vertex(T)的總flow為\(8\)單位。
• 若要找「還能夠增加多少流量」，也就是找Augmenting Paths，需要在Residual Networks上找，如圖四(c)右。
  • 若在\(Path:S-A-B-T\)、\(Path:S-A-C-D-T\)、\(Path:S-C-B-T\)流入「不超過該路徑上最低residual capacity」之flow，都是圖四(c)上的Augmenting Paths。

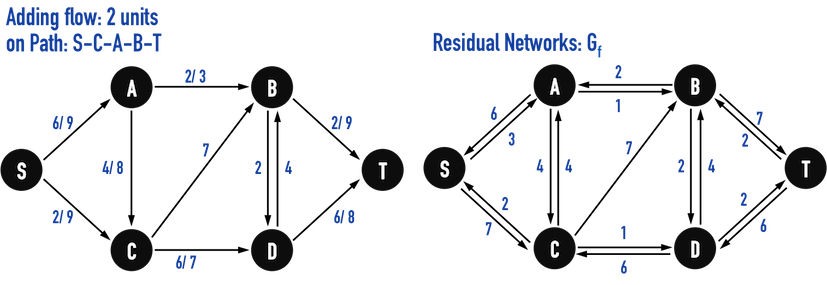
圖四(c)。

演算法概念

Ford-Fulkerson Algorithm(若使用BFS搜尋路徑，又稱為Edmonds-Karp Algorithm的方法如下：

• 在Residual Networks上尋找Augmenting Paths。
  • 若以BFS()尋找，便能確保每次找到的Augmenting Paths一定經過「最少的edge」。
  • 找到Augmenting Paths上的「最小residual capacity」加入總flow。
  • 再以「最小residual capacity」更新Residual Networks上的edge之residual capacity。
• 重複上述步驟，直到再也沒有Augmenting Paths為止。

便能找到Maximum Flow。

以圖二(a)之Flow Networks作為範例，尋找Maximum Flow之步驟如下：

• 先以「flow為零」對residual networks進行初始化，如圖五(a)。
  觀察後發現，G_f就是Adjacency Matrix。

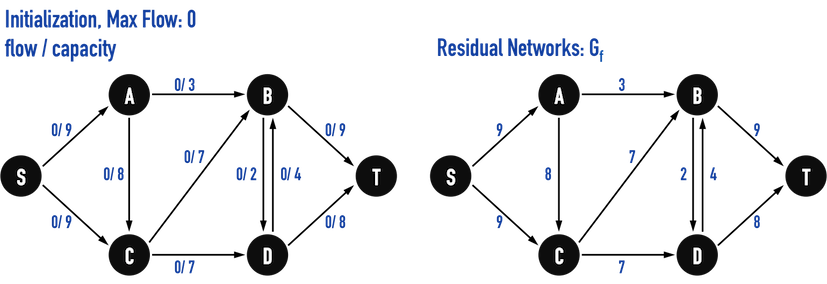
圖五(a)。

• 在G_f上，以BFS()找到能夠從vertex(S)走到vertex(T)，且「egde數最少」的路徑：\(Path:S-A-B-T\)，見圖五(b)。
  • 根據「Graph上建立vertex的順序」，BFS()有可能找到都是\(3\)條edge的\(Path:S-A-B-T\)或是\(Path:S-C-D-T\)。這裡以前者為例。

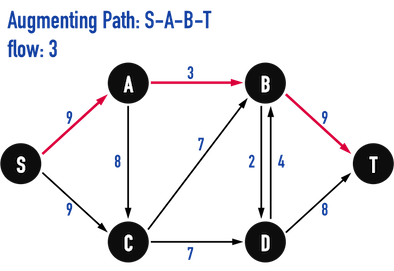
圖五(b)。

• 觀察\(Path:S-A-B-T\)上之edge，發現edge(A,B)具有「最小residual capacity」，\(c_f(A,B)=3\)，便更新「總flow新增\(3\)」。

• G_f上，更新edge之residual capacity，見圖五(c)：

  • \(c_f(S,A)=c(S,A)-f(S,A)=9-3=6\)
  • \(c_f(A,S)=c(A,S)-f(A,S)=0+3=3\)
  • \(c_f(A,B)=c(A,B)-f(A,B)=3-3=0\)
  • \(c_f(B,A)=c(B,A)-f(B,A)=0+3=3\)
  • \(c_f(B,T)=c(B,T)-f(B,T)=9-3=6\)
  • \(c_f(T,B)=c(T,B)-f(T,B)=0+3=3\)

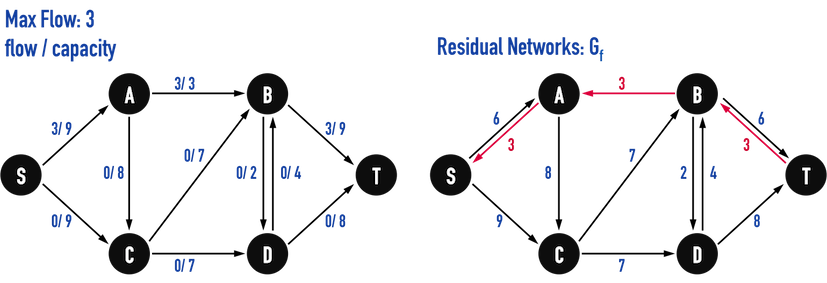
圖五(c)。

• 在G_f上，以BFS()找到能夠從vertex(S)走到vertex(T)，且「egde數最少」的路徑：\(Path:S-C-D-T\)，見圖五(d)。

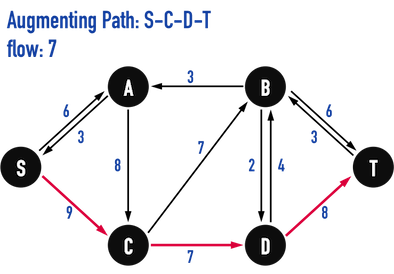
圖五(d)。

• 觀察\(Path:S-A-B-T\)上之edge，發現edge(C,D)具有「最小residual capacity」，\(c_f(C,D)=7\)，便更新「總flow新增\(7\)」。

• G_f上，更新edge之residual capacity，見圖五(e)：

  • \(c_f(S,C)=c(S,C)-f(S,C)=9-7=2\)
  • \(c_f(C,S)=c(C,S)-f(C,S)=0+7=7\)
  • \(c_f(C,D)=c(C,D)-f(C,D)=7-7=0\)
  • \(c_f(D,C)=c(D,C)-f(D,C)=0+7=7\)
  • \(c_f(D,T)=c(D,T)-f(D,T)=8-7=1\)
  • \(c_f(T,D)=c(T,D)-f(T,D)=0+7=7\)

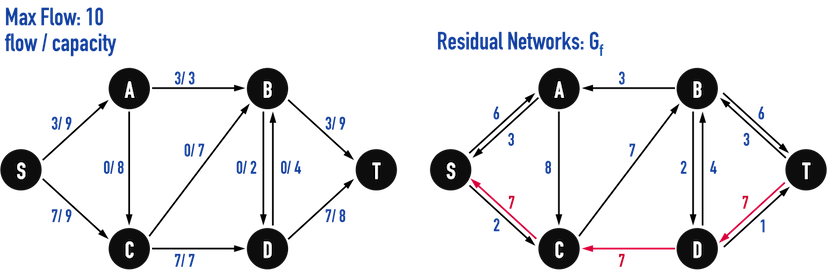
圖五(e)。

接著繼續重複上述步驟：「更新Residual Networks，尋找Augmenting Paths」，見圖五(f)-(l)。

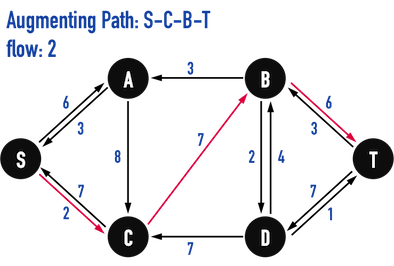
圖五(f)：找到\(Path:S-C-B-T\)。

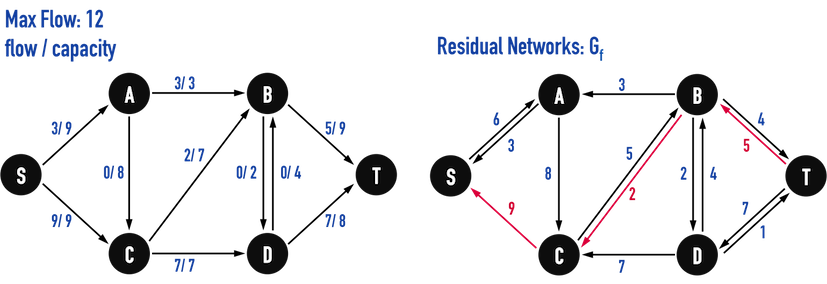
圖五(g)：更新Residual Networks。

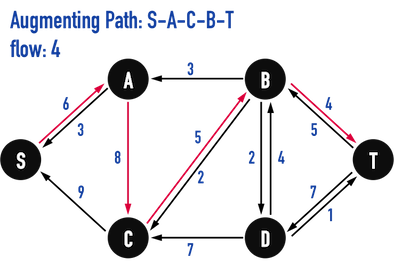
圖五(h)：找到\(Path:S-A-C-B-T\)。

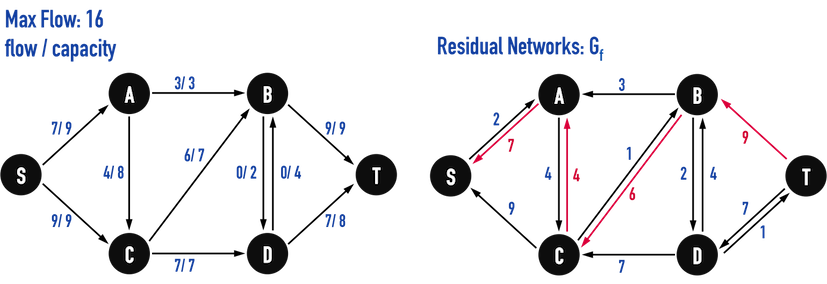
圖五(i)：更新Residual Networks。

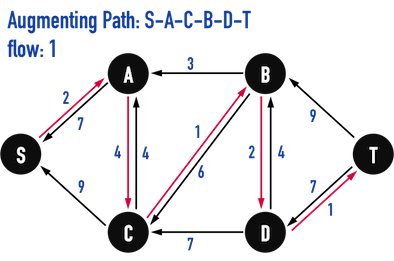
圖五(j)：找到\(Path:S-A-C-B-D-T\)。

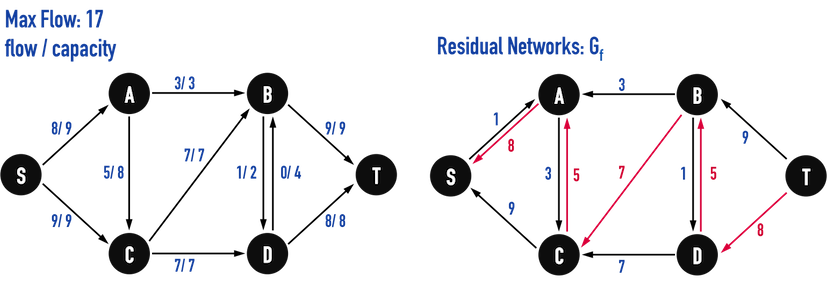
圖五(k)：更新Residual Networks。

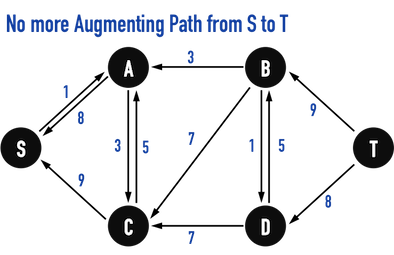
圖五(l)：找到Maximum Flow。

當執行到圖五(l)，在Residual Networks上再也找不到任何一條Augmenting Paths，便完成演算法。
Maximum Flow為\(17\)。

程式碼

程式碼包含幾個部分：

class Graph_FlowNetWorks：

• 使用AdjMatrix建立Graph，並利用AdjMatrix[X][Y]儲存edge(X,Y)的weight。
• BFSfindExistingPath()：利用Breadth-First Search尋找「從source走到termination」的路徑，而且是edge數最少的路徑。
  • 關於Breadth-First Search，請參考Graph: Breadth-First Search(BFS，廣度優先搜尋)。
• FordFulkerson()：進行Ford-Fulkerson Algorithm的主要函式，內容如前一小節所述。
• MinCapacity()：用來找到從BFSfindExistingPath()找到的路徑上，最小的residual capacity。

以及main()：建立如圖二(a)之AdjMatrix，並進行FordFulkerson()。

// C++ code
#include <iostream>
#include <vector>
#include <queue>

class Graph_FlowNetWorks{
private:
    int num_vertex;
    std::vector<std::vector<int>> AdjMatrix;
public:
    Graph_FlowNetWorks():num_vertex(0){};
    Graph_FlowNetWorks(int n);
    void AddEdge(int from, int to, int capacity);

    void FordFulkerson(int source, int termination);
    bool BFSfindExistingPath(std::vector<std::vector<int>> graphResidual, 
                             int *predecessor, int source, int termination);
    int MinCapacity(std::vector<std::vector<int>> graphResidual, 
                    int *predecessor, int termination);

};
Graph_FlowNetWorks::Graph_FlowNetWorks(int n):num_vertex(n){
    // constructor
    AdjMatrix.resize(num_vertex);
    for (int i = 0; i < num_vertex; i++)
        AdjMatrix[i].resize(num_vertex);
}

bool Graph_FlowNetWorks::BFSfindExistingPath(std::vector<std::vector<int>> graph, 
                                             int *predecessor, int s, int t){
    int visited[num_vertex];

    for (int i = 0; i < num_vertex; i++){
        visited[i] = 0;     // 0 表示還沒有被找到
        predecessor[i] = -1;
    }

    std::queue<int> queue;
    // BFS 從 s 開始, 也可以規定s一律訂成vertex(0)
    queue.push(s);
    visited[s] = 1;
    while (!queue.empty()) {
        int exploring = queue.front();
        for (int j = 0; j < num_vertex; j++) {
            if (graph[exploring][j]!=0 && visited[j]==0) {
                queue.push(j);
                visited[j] = 1;
                predecessor[j] = exploring;
            }
        }
        queue.pop();
    }
    return (visited[t] == 1);   // 若t有被visited, 表示有path從s到t
                                // 也可以用 if (predecessor[t] != -1) 判斷
}

int Graph_FlowNetWorks::MinCapacity(std::vector<std::vector<int>> graph, 
                                    int *predecessor, int t){
    int min = 100;      // 確保min會更新, 假設graph上的capacity都小於100

    // 用predecessor[idx] 和 idx 表示一條edge
    // 找到在從s到t的path上, capacity最小的值, 存入min
    for (int idx = t; predecessor[idx] != -1; idx = predecessor[idx]){
        if (graph[predecessor[idx]][idx]!=0 && graph[predecessor[idx]][idx] < min) {
            min = graph[predecessor[idx]][idx];
        }
    }
    return min;
}

void Graph_FlowNetWorks::FordFulkerson(int source, int termination){

    // residual networks的初始狀態等於AdjMatrix, 見圖五(a)
    std::vector<std::vector<int>> graphResidual(AdjMatrix);    
    int maxflow = 0;                                           
    int predecessor[num_vertex];

    // BFS finds augmenting path,
    while (BFSfindExistingPath(graphResidual, predecessor, source, termination)) {
        int mincapacity = MinCapacity(graphResidual, predecessor, termination);
        maxflow = maxflow + mincapacity;
        for (int Y = termination; Y != source; Y = predecessor[Y]){
            // 更新 residual graph
            int X = predecessor[Y];
            graphResidual[X][Y] -= mincapacity;
            graphResidual[Y][X] += mincapacity;
        }
    }
    std::cout << "Possible Maximum Flow: " << maxflow << std::endl;
}
void Graph_FlowNetWorks::AddEdge(int from, int to, int capacity){

    AdjMatrix[from][to] = capacity;
}

int main(){
    Graph_FlowNetWorks g11(6);

    g11.AddEdge(0, 1, 9);g11.AddEdge(0, 3, 9);
    g11.AddEdge(1, 2, 3);g11.AddEdge(1, 3, 8);
    g11.AddEdge(2, 4, 2);g11.AddEdge(2, 5, 9);
    g11.AddEdge(3, 2, 7);g11.AddEdge(3, 4, 7);
    g11.AddEdge(4, 2, 4);g11.AddEdge(4, 5, 8);

    g11.FordFulkerson(0, 5);    // 指定source為vertex(0), termination為vertex(5)
    return 0;
}

output:

Possible Maximum Flow: 17

結果與圖五(k)相同。

利用BFS的優點

若在Residual Networks尋找Augmenting Paths的方法中，

• 沒有用上BFS，稱為Ford-Fulkerson Algorithm，時間複雜度\(O(E|f|)\)。
  • 其中，\(E\)為Graph上的edge數；
  • \(|f|\)為「最大流量」。
• 有用上BFS，稱為Edmonds-Karp Algorithm，時間複雜度\(O(VE^2)\)。

顯然，使用BFS的優勢在於時間複雜度。
嚴謹證明請參考David Mix Barrington：The Edmonds-Karp Heuristic。
以下僅以一個簡單的例子，奉勸讀者使用BFS沒有害處。

以圖六(a)為例，若使用BFS，Maximum Flow只需要「找兩次」Augmenting Paths，\(Path:S-A-T\)以及\(Path:S-C-T\)。

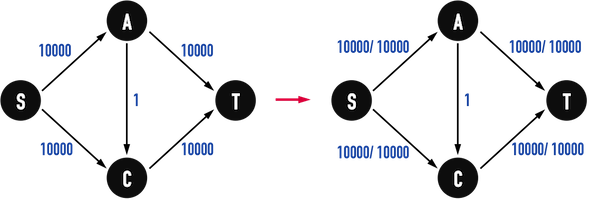
圖六(a)。

但如果使用DFS()或其他方法，很有可能找到\(Path:S-A-C-T\)，因為edge(A,C)的capacity只有\(1\)，\(c(A,C)=1\)，便限制了每單位時間的流量，見圖六(b)。

若不幸，在下一次挑選Augmenting Paths時，選到\(Path:S-C-A-T\)，又只能流入\(1\)單位的flow。
若每次都挑選到capacity只有\(1\)的edge，那麼，總共尋找Augmenting Paths的次數恰等於「總flow」的量，以圖六(b)為例，需要找\(20000\)次Augmenting Paths，不算有效率的方法。

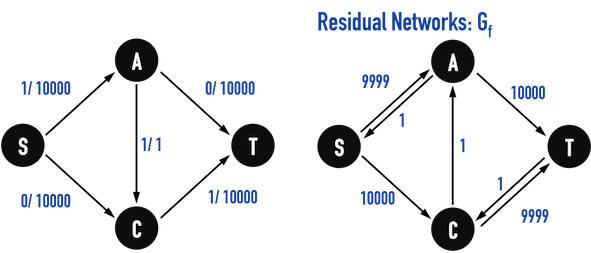
圖六(b)。

以上便是Ford-Fulkerson Algorithm(說是Edmonds-Karp Algorithm也可以)的介紹。
關於Maximum Flow的應用，請參考Wikipedia：Maximum flow problem。

參考資料：

• Introduction to Algorithms, Ch26
• Fundamentals of Data Structures in C++, Ch6
• LILD：Ford Fulkerson algorithm for Max Flow
• GeeksforGeeks：Ford-Fulkerson Algorithm for Maximum Flow Problem
• Graph: Breadth-First Search(BFS，廣度優先搜尋)
• David Mix Barrington：The Edmonds-Karp Heuristic
• Wikipedia：Maximum flow problem
• Mr. Opengate：Algorithm - Ch5 網路流 與 最大流最小割定理 Network Flow and Maximum Flow Minimum Cut Theorem
• CK6125姜俊宇：網路流(Network Flow)

Flow Networks系列文章

Flow Networks：Maximum Flow & Ford-Fulkerson Algorithm

回到目錄：

目錄：演算法與資料結構