Single-Source Shortest Path：on DAG(directed acyclic graph)

先備知識與注意事項

本篇文章將介紹在DAG(directed acyclic graph)上處理Single-Source Shortest Path問題之演算法，除了DAG之外，與之息息相關的Topological Sort也會跑出來，再加上Path-Relaxation Property，就能建構起本篇文章的演算法核心。

名詞概念回顧

DAG(directed acyclic graph)

所謂的DAG(directed acyclic graph)，就是不存在cycle的directed graph，如圖一(a)與圖一(b)：

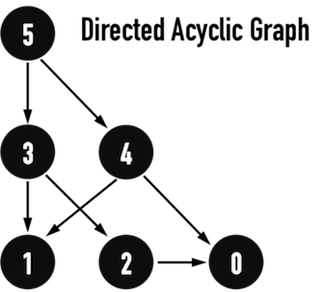
圖一(a)。

圖一(b)。

Topological Sort

若在DAG上，存在一條從vertex(X)指向vertex(Y)的edge(X,Y)，那麼在Topological Sort中，vertex(X)一定出現在vertex(Y)之前。
(關於DAG與Topological Sort的詳細介紹與演算法，請參考Graph: 利用DFS尋找DAG的Topological Sort(拓撲排序)。)

試尋找圖一(a)之DAG的Topological Sort，如圖二(a)。可以確定的是，Topological Sort可能不唯一。

圖二(a)之Graph存在edge(4,1)，因此在Topological Sort中vertex(4)一定在vertex(1)之前。依此類推，可以觀察其餘vertex在Topological Sort裡的相互關係。

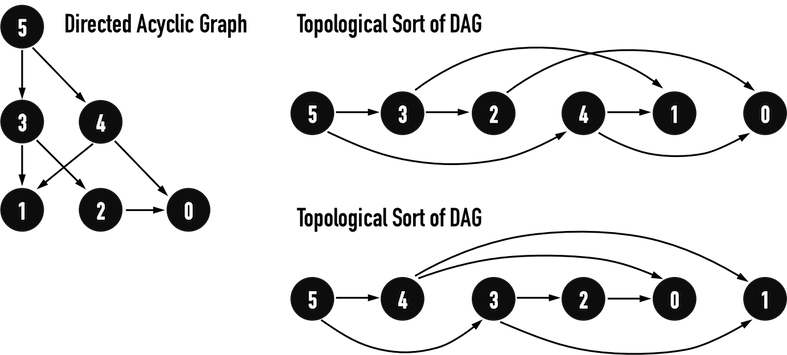
圖二(a)。

圖二(b)為圖一(b)之DAG的Topological Sort。

圖二(b)。

Path-Relaxation Property

根據Path-Relaxation Property：若從vertex(0)走到vertex(3)之最短路徑為\(Path:0-1-2-3\)，那麼只要在對edge進行Relaxation的順序出現「edge(0,1)\(-\)edge(1,2)\(-\)edge(2,3)」的順序，不管其他edge(0,2)、edge(1,3)是否也有進行Relaxation，distance[3]一定能夠更新至最短路徑\(Path:0-1-2-3\)的weight，distance[3]\(=\delta(0,3)=w(0,1)+w(1,2)+w(2,3)\)。

(詳細定義請參考Single-Source Shortest Path：Intro(簡介)。)

圖三。

Single-Source Shortest Path in DAG

有了以上概念之後，要在DAG上找到Single-Source Shortest Path就變得輕鬆寫意了：

找到DAG的Topological Sort；
按照Topological Sort的vertex順序，對所有從該vertex出發連接至其餘vertex的edge進行Relaxation。
大功告成。

為什麼這樣可行？

因為在DAG中，不存在cycle(若從vertex(X)離開後，就不可能再回到vertex(X))，所以路徑只有「一個方向」，因此最短路徑的方向一定也依循著DAG的「大方向」。以圖四(a)為例，DAG的「大方向」即為「由左至右」，從vertex(0)至vertex(6)。

而Topological Sort會把vertex按照「大方向的頭到尾」之順序排列，若按照此vertex順序，對所有與此vertex相連之edge進行Relax()，就會從最短路徑的最前端edge開始，一路往最短路徑之尾端edge進行Relax()，如此便滿足Path-Relaxation Property，因此，以上演算法可以得到最短路徑。

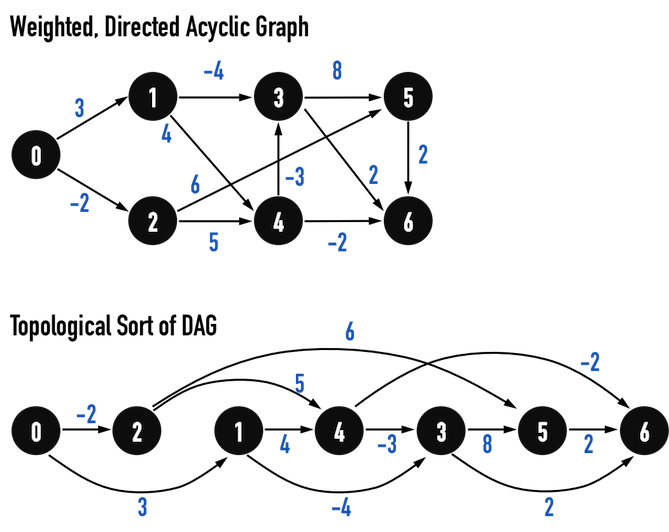
圖四(a)。

以下便按照上述演算法，在圖四(a)之DAG上找到Single-Source問題之最短路徑，見圖四(b)-(g)。

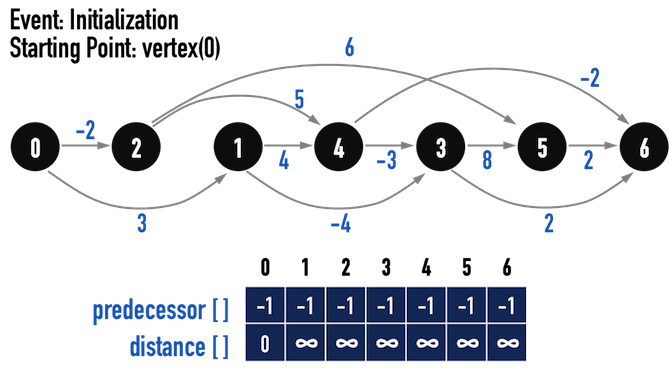
圖四(b)。

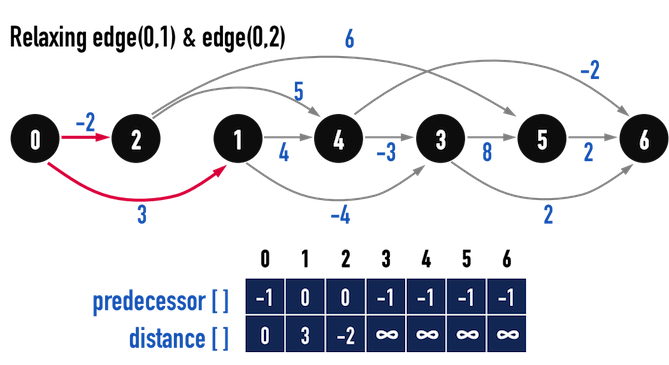
圖四(c)。

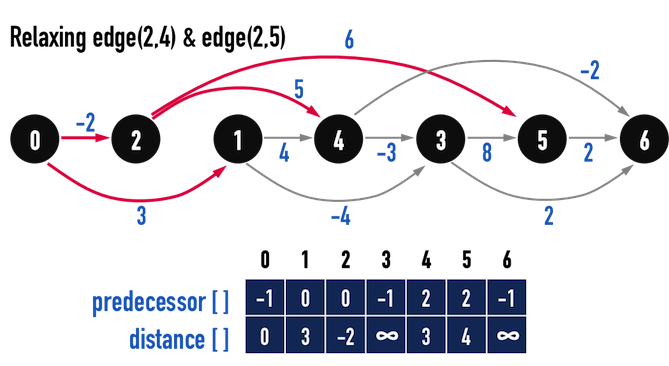
圖四(d)。

圖四(e)。

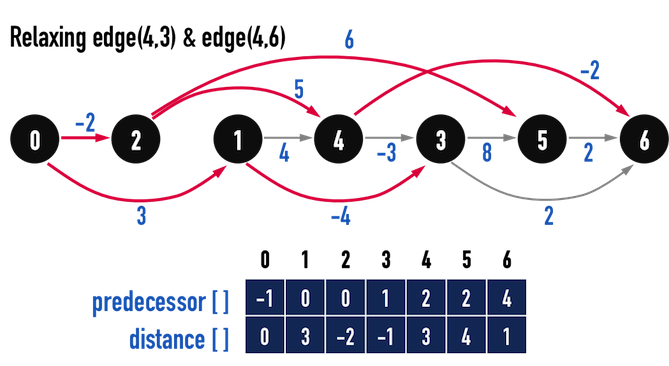
圖四(f)。

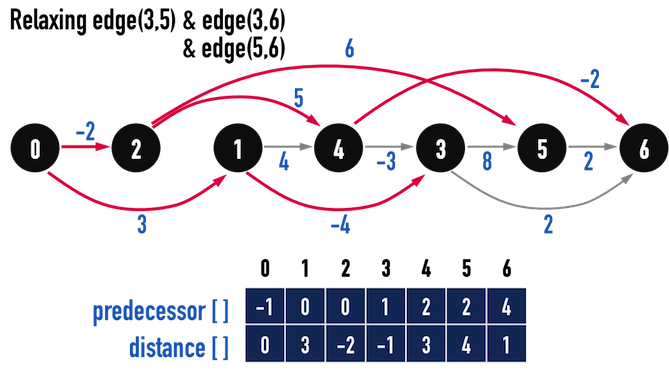
圖四(g)。

最後，由以上演算法找到的Predecessor Subgraph如圖四(h)：

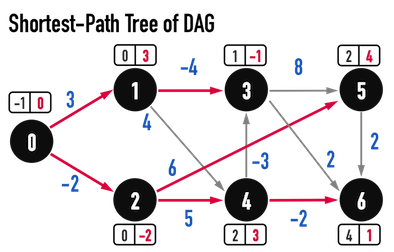
圖四(g)。

程式碼

範例程式碼中包含：

class Graph_SP：

基本的資料項目：predecessor、distance、num_vertex、AdjList。
Relax()、InitializeSingleSource()之功能與Bellman-Ford Algorithm所使用相同。
DAG_SP()：尋找Shortest-Path Tree的主要函式，功能如前一小節所述。
GetTopologicalSort()：可以視為DFS()的變形，主要功能是建立color[]、discover[]、finish[]等資料項目，並把從DAG_SP()接收來的資料項目topologicalsort[]傳進DFSVisit_TS()。
順便在找到topologicalsort[]後，將discover[]與finish[]印出。
DFSVisit_TS()：此為DFSVisit()的變形，唯一修改的部分是在finish[]更新後，多加了一行array[count--] = vertex;，其中count為topologicalsort[]的index，用意是要按照「探索結束」的先後，將vertex依序從topologicalsort[]的尾端放到前端，如此一來，topologicalsort[]所存放的vertex，就會按照finish[]由大到小的順序。

以及main()：建立如圖四(a)之AdjList，並進行DAG_SP()。

(關於DFS()與DFSVisit()之概念與程式碼，請參考Graph: Depth-First Search(DFS，深度優先搜尋)。)
(關於Topological Sort與DFS()的關聯，請參考Graph: 利用DFS尋找DAG的Topological Sort(拓撲排序)。)

// C++ code
#include <iostream>
#include <vector>
#include <list>
#include <utility>          // for std::pair<>
#include <iomanip>          // for std::setw()

const int Max_Distance = 100;
class Graph_SP{             // SP serves as Shortest Path
private:
    int num_vertex;
    std::vector<std::list<std::pair<int,int>>> AdjList;
    std::vector<int> predecessor, distance;
public:
    Graph_SP():num_vertex(0){};
    Graph_SP(int n):num_vertex(n){
        AdjList.resize(num_vertex);
    }
    void AddEdge(int from, int to, int weight);
    void PrintDataArray(std::vector<int> array);
    void PrintIntArray(int *array);

    void InitializeSingleSource(int Start);     // 以Start作為起點
    void Relax(int X, int Y, int weight);       // 對edge(X,Y)進行Relax

    void DAG_SP(int Start = 0);                     // 需要 DFS, 加一個額外的Linked list
    void GetTopologicalSort(int *array, int Start);
    void DFSVisit_TS(int *array, int *color, int *discover, 
                     int *finish, int vertex, int &time, int &count);

};
void Graph_SP::GetTopologicalSort(int *array, int Start){

    int color[num_vertex], discover[num_vertex], finish[num_vertex];

    for (int i = 0; i < num_vertex; i++) {
        color[i] = 0;
        discover[i] = 0;
        finish[i] = 0;
        predecessor[i] = -1;
    }

    int time = 0,
        count = num_vertex-1,        // count 為 topologicalsort[] 的 index
        i = Start;

    for (int j = 0; j < num_vertex; j++) {
        if (color[i] == 0) {
            DFSVisit_TS(array, color, discover, finish, i, time, count);
        }
        i = j;
    }
    std::cout << "\nprint discover time:\n";
    PrintIntArray(discover);
    std::cout << "\nprint finish time:\n";
    PrintIntArray(finish);
}
void Graph_SP::DFSVisit_TS(int *array, int *color, int *discover, 
                           int *finish, int vertex, int &time, int &count){

    color[vertex] = 1;  // set gray
    discover[vertex] = ++time;
    for (std::list<std::pair<int,int>>::iterator itr = AdjList[vertex].begin(); 
         itr != AdjList[vertex].end(); itr++) {
        if (color[(*itr).first] == 0) {
            predecessor[(*itr).first] = vertex;
            DFSVisit_TS(array, color, discover, finish, (*itr).first, time, count);
        }
    }
    color[vertex] = 2;  // set black
    finish[vertex] = ++time;
    array[count--] = vertex;            // 產生Topological Sort
}
void Graph_SP::DAG_SP(int Start){

    InitializeSingleSource(Start);      // distance[],predecessor[]的initialization

    int topologicalsort[num_vertex];
    GetTopologicalSort(topologicalsort, Start);

    for (int i = 0; i < num_vertex; i++) {
        int v = topologicalsort[i];
        for (std::list<std::pair<int, int>>::iterator itr = AdjList[v].begin();
             itr != AdjList[v].end(); itr++) {
            Relax(v, (*itr).first, (*itr).second);
        }
    }
    std::cout << "\nprint predecessor:\n";
    PrintDataArray(predecessor);
    std::cout << "\nprint distance:\n";
    PrintDataArray(distance);
}
void Graph_SP::PrintDataArray(std::vector<int> array){
    for (int i = 0; i < num_vertex; i++)
        std::cout << std::setw(4) << i;
    std::cout << std::endl;
    for (int i = 0; i < num_vertex; i++)
        std::cout << std::setw(4) << array[i];
    std::cout << std::endl;
}
void Graph_SP::PrintIntArray(int *array){
    for (int i = 0; i < num_vertex; i++)
        std::cout << std::setw(4) << i;
    std::cout << std::endl;
    for (int i = 0; i < num_vertex; i++)
        std::cout << std::setw(4) << array[i];
    std::cout << std::endl;
}
void Graph_SP::InitializeSingleSource(int Start){

    distance.resize(num_vertex);
    predecessor.resize(num_vertex);

    for (int i = 0; i < num_vertex; i++) {
        distance[i] = Max_Distance;
        predecessor[i] = -1;
    }
    distance[Start] = 0;
}
void Graph_SP::Relax(int from, int to, int weight){

    if (distance[to] > distance[from] + weight) {
        distance[to] = distance[from] + weight;
        predecessor[to] = from;
    }
}
void Graph_SP::AddEdge(int from, int to, int weight){
    AdjList[from].push_back(std::make_pair(to,weight));
}

int main(){

    Graph_SP g8(7);
    g8.AddEdge(0, 1, 3);g8.AddEdge(0, 2, -2);
    g8.AddEdge(1, 3, -4);g8.AddEdge(1, 4, 4);
    g8.AddEdge(2, 4, 5);g8.AddEdge(2, 5, 6);
    g8.AddEdge(3, 5, 8);g8.AddEdge(3, 6, 2);
    g8.AddEdge(4, 3, -3);g8.AddEdge(4, 6, -2);
    g8.AddEdge(5, 6, 2);

    g8.DAG_SP(0);        // 以vertex(0)作為起點

    return 0;
}

output:

print discover time:
   0   1   2   3   4   5   6
   1   2  12   3   9   4   5

print finish time:
   0   1   2   3   4   5   6
  14  11  13   8  10   7   6

print predecessor:
   0   1   2   3   4   5   6
  -1   0   0   1   2   2   4

print distance:
   0   1   2   3   4   5   6
   0   3  -2  -1   3   4   1

以上結果符合圖四(g)的預期。

若嘗試以vertex(2)作為起點：

int main(){
    ...
    g8.DAG_SP(2);

    return 0;
}

output:

print discover time:
   0   1   2   3   4   5   6
  11  12   1   3   2   4   5

print finish time:
   0   1   2   3   4   5   6
  14  13  10   8   9   7   6

print predecessor:
   0   1   2   3   4   5   6
  -1   0  -1   4   2   2   4

print distance:
   0   1   2   3   4   5   6
 100 100   0   2   5   6   3

結果便如圖五，因為從vertex(2)走不到vertex(0)與vertex(1)，因此distance[0]與distance[1]仍維持起始值無限大(範例程式將無限大設為\(100\))。

圖五。

以上便是在DAG(directed acyclic graph)中處理Single-Source Shortest Path之演算法之介紹。
同樣地，只要了解：

Relaxation
Convergence property
Path-relaxation property

之概念，即可掌握此演算法的運作邏輯。

下一篇文章將介紹大魔王：Dijkstra's Algorithm，如果讀者熟悉Prim's Algorithm的話，可能會有些幫助。

參考資料：

Shortest Path系列文章

Shortest Path：Intro(簡介)
Single-Source Shortest Path：Bellman-Ford Algorithm
Single-Source Shortest Path：on DAG(directed acyclic graph)
Single-Source Shortest Path：Dijkstra's Algorithm
All-Pairs Shortest Path：Floyd-Warshall Algorithm

回到目錄：

目錄：演算法與資料結構