先備知識與注意事項
在Binary Tree: Traversal(尋訪)中介紹過Pre-Order Traversal,其Visiting順序:「Current(V)-left(L)-right(R)」可以解讀成「先遇到的node就先Visiting」,因此,每一組「Current-left-right」必定是CurrentNode先Visiting,接著是leftchild,最後才是rightchild。
若對圖一中的Binary Tree進行Pre-Order Traversal,定義Visiting為印出(print)資料,將得到:
A B D E G H C F

圖一。
Depth-First Search(DFS,深度優先搜尋)的核心精神便如同Pre-Order Traversal:「先遇到的vertex就先Visiting」,並且以先遇到的vertex作為新的搜尋起點,直到所有「有edge相連的vertex」都被探索過。
以圖二的迷宮為例,把迷宮矩陣中的每一格定義成一個vertex,若兩個vertex之間有路,則建立edge相連。若要在迷宮中尋找抵達終點的路線,通常會先選擇其中一條路線,只要有路就繼續往前走。有可能一路走到終點,也有可能遇到死路。若遇到死路則回到上一個岔路,往另一條路探索路線。依此類推,直到走出迷宮。

圖二:迷宮問題(maze problem)。
目錄
Depth-First Search(DFS,深度優先搜尋)
考慮圖三(a)的Graph(沒有weight的directed graph):

圖三(a):。
若以vertex(A)為起點進行DFS(),可以得到:
- 若Graph中的vertex與vertex(A)之間存在至少一條path,則
DFS()必定能找到其中一條path從vertex(A)抵達該vertex。但是這條path未必保證是最短路徑(shortest path)。
看起來好像沒有BFS()這麼殺手級,雖然找到一條路卻不保證是最短路徑。
但其實DFS()還是很有用的,因為經過一次DFS()後,將得到一項資料稱作finish,而finish竟然可以用來...!?
別轉台,看下去。
演算法
以下介紹的DFS()需要資料項目共有:
time:在整個DFS()的過程會有一條「時間軸」,若Graph中有\(N\)個vertex,「時間軸」上一共會有\(2N\)個「時間點」。discover與finisharray:每個vertex會被標記上兩個「時間點」,分別是「被發現(discover)」的時間與「結束(finish)」的時間:discover:例如,vertex(B)被vertex(A)找到,則discover[B]會是discover[A]加一,表示vertex(B)在整個時間軸上是在vertex(A)之後被找到(這其中便存在「ancestor-descendant」的關係)。finish:若vertex(B)已經經由有效edge探索過所有與之相連的vertex,表示以vertex(B)為起點的探索已經結束,便標上finish[B]。
colorarray:利用color標記哪些vertex已經「被發現」與「結束」。- 白色表示該vertex還沒有「被發現」;
- 灰色表示該vertex已經「被發現」,但是還沒有「結束」。
- 黑色表示該vertex已經「結束」。
predecessorarray:記錄某個vertex是被哪一個vertex找到的,如此便能回溯路徑(如同BFS(),DFS()亦能生成一個Predecessor Subgraph)。
DFS()的方法如下:
初始化(initialization),見圖三(b):
- 先把
time設為0,表示還沒有任何vertex「被發現」。 - 把所有vertex塗成白色。
- 把所有vertex的
predecessor清除(或者設成NULL、-1,視資料形態(data type)而定)。 - 把所有vertex的
discover與finish設成0,表示還沒有開始進行DFS()。

圖三(b):。
以vertex(A)作為起點,見圖三(c):
- 將vertex(A)塗成灰色,表示已經「被發現」。
- 由於vertex(A)已經「被發現」,便把
discover[A]設為++time。原本time=0,而vertex(A)是DFS()的起點,所以++time之後distance[A]=1便表示vertex(A)是第一個被發現。 - 接著尋找所有與vertex(A)相連之vertex,只要遇到第一個仍為白色的vertex,便把該vertex設為新的搜尋起點,並將該vertex之
predecessor設為vertex(A)。- 圖三(a)之
Adjacency List中,第一個與vertex(A)相連的vertex為vertex(B),接著便以vertex(B)為起點,繼續尋找與vertex(B)相連之「最近的」vertex。
- 圖三(a)之
- 由於從vertex(A)找到了vertex(B),便表示「從vertex(A)出發的path」還在更新,於是vertex(A)便還沒有「結束」,所以
finish[A]不需要更新。- 那麼,什麼時候會更新
finish[A]呢?
在Adjacency List中,與vertex(A)相連之vertex有vertex(B)與vertex(C),要在這兩個vertex都「作為搜尋起點」,並且「探索完所有相連的vertex」後(也就是更新完finish[B]與finish[C]後),才會更新到finish[A]。
- 那麼,什麼時候會更新
- 圖三(c)中的「Time Stamp(時間戳記)」即為「時間軸」。
此時進入「剛發現vertex(A)」,並且尚未結束「以vertex(A)作為搜尋起點」的階段。

圖三(c):。
從vertex(A)作為探索起點,「最先發現」的是vertex(B),便以其作為新的起點:
- 把vertex(B)塗成灰色,表示已經「被發現」。
- 由於vertex(B)已經「被發現」,便把
discover[B]設為++time,也就是distance[B]=2。 - 接著,找到
Adjacency List中第一個與vertex(B)相連,且為白色的vertex(D),將vertex(D)視為新的搜尋起點。 - 此時圖三(d)的「時間軸」表示,「以vertex(A)作為起點」之搜尋尚未結束(vertex(A)還沒有被塗黑),而且「以vertex(B)作為起點」之搜尋剛剛開始。

圖三(d):。
來到「以vertex(D)作為起點」之搜尋,大致上與「以vertex(B)作為起點」之搜尋相同:
- 把vertex(D)塗成灰色,表示已經「被發現」。
- 由於vertex(D)已經「被發現」,便把
discover[D]設為++time,也就是distance[D]=3。 - 接著,找到
Adjacency List中第一個與vertex(D)相連,且為白色的vertex(E),將vertex(E)視為新的搜尋起點。 - 此時圖三(e)的「時間軸」表示,「以vertex(A)與vertex(B)作為起點」之搜尋都還沒結束(vertex(A)、vertex(B)還沒有被塗黑),而且「以vertex(D)作為起點」之搜尋剛剛開始。

圖三(e):。
來到「以vertex(E)作為起點」之搜尋,與前兩個步驟相同,不再贅述,見圖三(f)。

圖三(f):。
關鍵是圖三(g)。
當vertex(E)再也找不到任何「能夠抵達、且為白色」的vertex時(見圖三(g)中Graph的箭頭方向,並對照圖三(a)之Adjacency List),就表示「以vertex(E)作為起點」之搜尋已經「結束」,此時:
- 把vertex(E)塗成黑色,表示「以vertex(E)作為起點」之搜尋已經「結束」。
- 把
finish[E]設成++time。- 原先在vertex(E)「被發現」時
time=4,更新後,表示vertex(E)之搜尋在time=5時「結束」。
- 原先在vertex(E)「被發現」時
- 當vertex(E)「結束」後,便回到vertex(E)的
predecessor,也就是「發現vertex(E)」的vertex(D),繼續探索其他vertex(D)能夠走到的vertex。 - 此時,圖三(g)的「時間軸」表示,
discover[E]=4,finish[E]=5,往後搜尋過程就不會再有vertex(E)出現。而以vertex(A)、vertex(B)、vertex(D)作為起點的搜尋則持續進行。

圖三(g):。
接著,從vertex(E)退回到vertex(D),並從vertex(D)繼續發現vertex(F)還是白色,於是便以「vertex(F)作為起點」進行搜尋:
- 把vertex(F)塗成灰色。
- 把
discover[F]設為++time。 - 繼續尋找所有從vertex(F)能夠走到,且為白色的vertex。

圖三(h):。
觀察圖三(i)的Graph與圖三(a)的Adjacency List,發現從vertex(F)能夠走到vertex(B),但是由於vertex(B)已經是「灰色」,表示「以vertex(B)為起點」之搜尋已經開始且尚未結束,於是vertex(F)無法「發現」vertex(B),也無法走到其餘vertex,所以,vertex(F)便宣告「結束」:
- 把vertex(F)塗成黑色,表示「以vertex(F)作為起點」之搜尋已經「結束」。
- 把
finish[F]設成++time。 - 當vertex(F)「結束」後,便回到vertex(F)的
predecessor,也就是「發現vertex(F)」的vertex(D),繼續探索其他vertex(D)能夠走到的vertex。

圖三(i):。
如圖三(j),所有vertex(D)能夠抵達的vertex都已經變成黑色,於是「以vertex(D)作為起點」之搜尋便結束:
- 把vertex(D)塗成黑色,表示「以vertex(D)作為起點」之搜尋已經「結束」。
- 把
finish[D]設成++time。 - 當vertex(D)「結束」後,便回到vertex(D)的
predecessor,也就是「發現vertex(D)」的vertex(B),繼續探索其他vertex(B)能夠走到的vertex。

圖三(j):。
接著便以上述邏輯重複步驟,直到vertex(A)被塗成黑色,見圖三(k)-(n)。

圖三(k):。
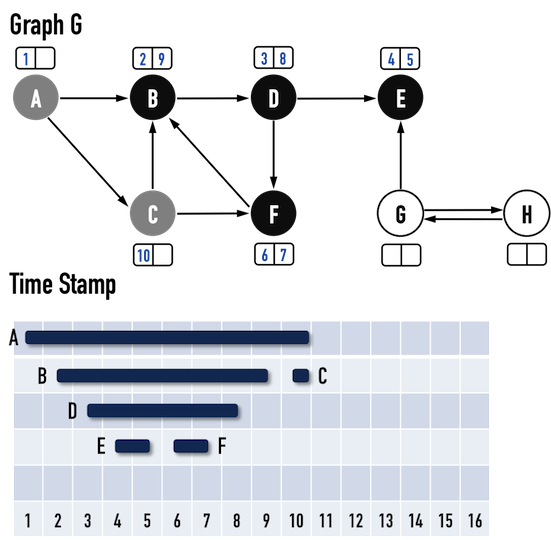
圖三(l):。
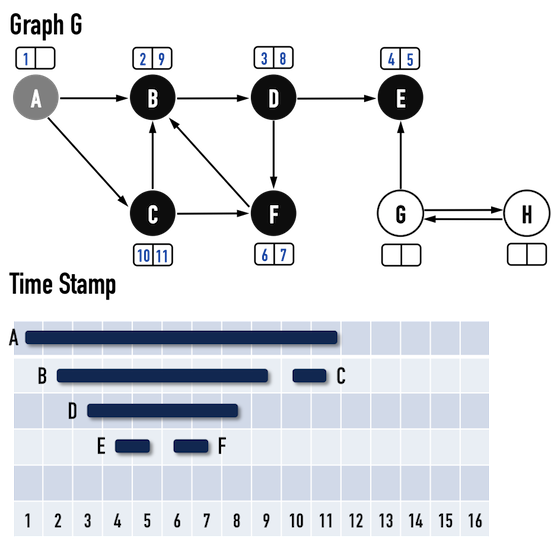
圖三(m):。
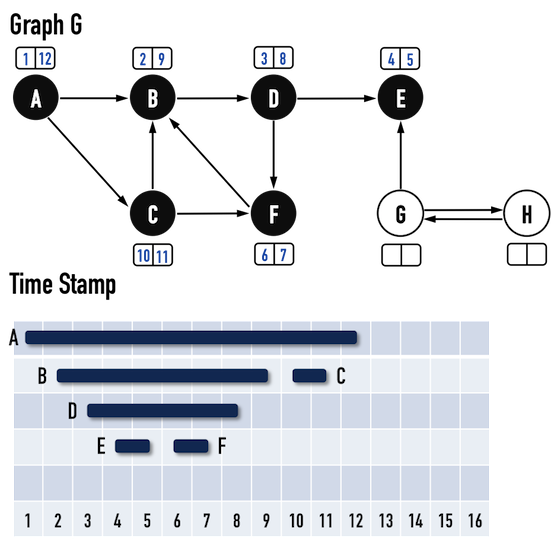
圖三(n):。
在「以vertex(A)為起點」之搜尋結束後,必須確認Graph中還有沒有白色的vertex,如圖三(n),Graph裡還有vertex(G)與vertex(H)仍然是白色,因此挑選其中一個vertex作為新的起點。這裡是按照Adjacency List的順序,由於vertex(G)在vertex(H)之前,便先挑選vertex(G),接著重複上述步驟,見圖三(o)-(r)。

圖三(o):。
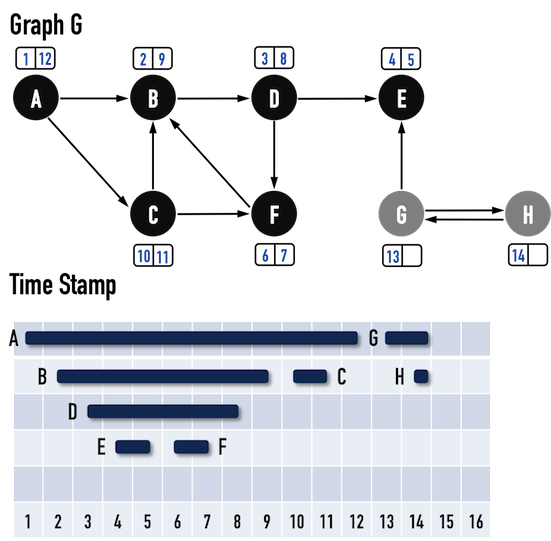
圖三(p):。
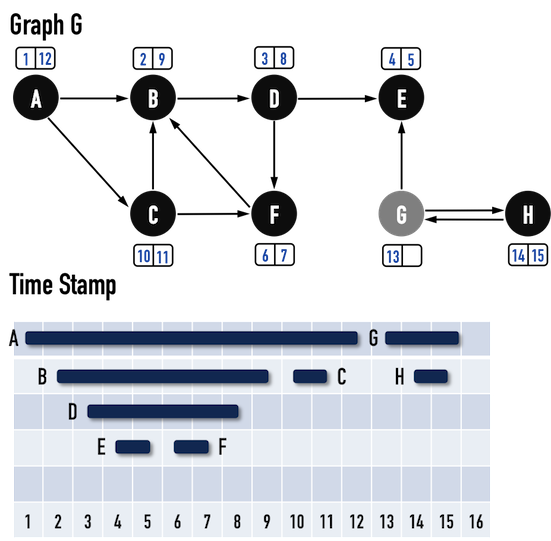
圖三(q):。
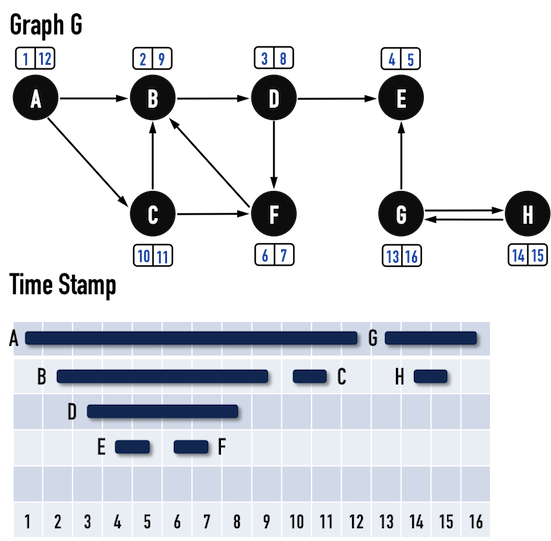
圖三(r):。
當Graph中所有vertex都被塗成黑色,便完成DFS()。
程式碼
由以上說明可以觀察出,DFS()本質上是一種「遞迴(recursion)結構」,而遞迴結構其實是利用了系統的「堆疊(stack)」,因此,這兩種方式皆能實現DFS(),以下提供的範例程式碼將以遞迴形式完成。
如同上一篇Graph: Breadth-First Search(BFS,廣度優先搜尋),以下將使用int處理資料,把\(9\)個vertexchar A~I依序對應到int 0~8。
範例程式碼包含兩個部分main()與class Graph。
在main()中,主要兩件事情:
- 建立如圖三(a)的
Adjacency List; - 進行
DFS()。
在class Graph中:
- private member:
num_vertex:需要在定義Graph的object(物件)時,給定vertex的數目,以便建立Adjacency List(或者Adjacency Matrix)。std::vector< std::list<int> > AdjList:利用C++標準函式庫(STL)提供的container(容器):std::vector與std::list來實現。color、discover、finish、predecessor:將在DFS()中使用,功能如上述。
- public member:
Constructor:Graph(int num_vertex):在定義Graph的object(物件)時,需要知道vertex的數目,並在constructor中定義好AdjList。AddEdgeList(int from, in to):功能便是在AdjList新增從from到to的edge。DFS(int Start):需要知道起點vertex。DFSVisit(int vertex, int &time):利用遞迴函式呼叫,進行color、discover、finish與predecessor等資料更新的主要函式。
// C++ code
#include <iostream>
#include <vector>
#include <list>
#include <queue>
#include <iomanip> // for std::setw()
class Graph{
private:
int num_vertex;
std::vector< std::list<int> > AdjList;
int *color, // 0:white, 1:gray, 2:black
*predecessor,
*discover,
*finish;
public:
Graph():num_vertex(0){};
Graph(int N):num_vertex(N){
// initialize Adj List
AdjList.resize(num_vertex);
};
void AddEdgeList(int from, int to);
void BFS(int Start); // 定義見上一篇文章
void DFS(int Start);
void DFSVisit(int vertex, int &time);
};
void Graph::DFS(int Start){
color = new int[num_vertex]; // 配置記憶體位置
discover = new int[num_vertex];
finish = new int[num_vertex];
predecessor = new int[num_vertex];
int time = 0; // 初始化, 如圖三(b)
for (int i = 0; i < num_vertex; i++) {
color[i] = 0;
discover[i] = 0;
finish[i] = 0;
predecessor[i] = -1;
}
int i = Start;
for (int j = 0; j < num_vertex; j++) { // 檢查所有Graph中的vertex都要被搜尋到
if (color[i] == 0) { // 若vertex不是白色, 則進行以該vertex作為起點之搜尋
DFSVisit(i, time);
}
i = j; // j會把AdjList完整走過一遍, 確保所有vertex都被搜尋過
}
}
void Graph::DFSVisit(int vertex, int &time){ // 一旦有vertex被發現而且是白色, 便進入DFSVisit()
color[vertex] = 1; // 把vertex塗成灰色
discover[vertex] = ++time; // 更新vertex的discover時間
for (std::list<int>::iterator itr = AdjList[vertex].begin(); // for loop參數太長
itr != AdjList[vertex].end(); itr++) { // 分成兩段
if (color[*itr] == 0) { // 若搜尋到白色的vertex
predecessor[*itr] = vertex; // 更新其predecessor
DFSVisit(*itr, time); // 立刻以其作為新的搜尋起點, 進入新的DFSVisit()
}
}
color[vertex] = 2; // 當vertex已經搜尋過所有與之相連的vertex後, 將其塗黑
finish[vertex] = ++time; // 並更新finish時間
}
int main(){
// 定義一個具有八個vertex的Graph
Graph g2(8);
// 建立如圖三之Graph
g2.AddEdgeList(0, 1);g2.AddEdgeList(0, 2);
g2.AddEdgeList(1, 3);
g2.AddEdgeList(2, 1);g2.AddEdgeList(2, 5);
g2.AddEdgeList(3, 4);g2.AddEdgeList(3, 5);
// AdjList[4] is empty
g2.AddEdgeList(5, 1);
g2.AddEdgeList(6, 4);g2.AddEdgeList(6, 7);
g2.AddEdgeList(7, 6);
g2.DFS(0); // 以vertex(0), 也就是vertex(A作為DFS()的起點
return 0;
}
討論
若在DFS()函式主體的最後多加入幾行程式來檢查predecessor、discover與finish三項資料是否符合預期:
void Graph::DFS(int Start){
// after for loop
std::cout << "predecessor:" << std::endl; // 印出 A(0) ~ H(7)的predecessor
for (int i = 0; i < num_vertex; i++){
std::cout << std::setw(4) << i;
}
std::cout << std::endl;
for (int i = 0; i < num_vertex; i++){
std::cout << std::setw(4) << predecessor[i];
}
std::cout << "\ndiscover time:" << std::endl; // 印出 A(0) ~ H(7)的discover time
for (int i = 0; i < num_vertex; i++){
std::cout << std::setw(4) << i;
}
std::cout << std::endl;
for (int i = 0; i < num_vertex; i++){
std::cout << std::setw(4) << discover[i];
}
std::cout << "\nfinish time:" << std::endl; // 印出 A(0) ~ H(7)的finish time
for (int i = 0; i < num_vertex; i++){
std::cout << std::setw(4) << i;
}
std::cout << std::endl;
for (int i = 0; i < num_vertex; i++){
std::cout << std::setw(4) << finish[i];
}
}
便能得到:
predecessor:
0 1 2 3 4 5 6 7
-1 0 0 1 3 3 -1 6
discover time:
0 1 2 3 4 5 6 7
1 2 10 3 4 6 13 14
finish time:
0 1 2 3 4 5 6 7
12 9 11 8 5 7 16 15
與預期的結果相同,如圖四。

圖四:。
Depth-First Tree
如同BFS(),在Graph上進行DFS()同樣可以得到Predecessor Subgraph,又稱為Depth-First Tree。若Graph本身不是(strongly) connected component,則有可能得到Depth-First Forest,如圖五:

圖五:。
根據圖五的「時間軸」,可以直接由discover與finish觀察出各個vertex之間的「ancestor-descendant」關係(也就包含了predecessor關係):
- 若
discover[X]比discover[Y]大,而且finish[X]比finish[Y]小,表示vertex(X)比vertex(Y)較晚「被發現」,而且較早「結束」,則vertex(X)必定是vertex(Y)的descendant。- 以vertex(E)與vertex(A)為例,vertex(E)的「搜尋生命週期」完全在vertex(A)的「搜尋生命週期」之內,因此vertex(E)必定是vertex(A)的descendant。
- 相反,若
discover[X]比discover[Y]小,而且finish[X]比finish[Y]大,表示vertex(X)比vertex(Y)較早「被發現」,而且較晚「結束」,則vertex(X)必定是vertex(Y)的ancestor。- 以vertex(B)與vertex(F)為例,vertex(B)的「搜尋生命週期」完全包覆住vertex(F)的「搜尋生命週期」,因此vertex(B)必定是vertex(F)的ancestor。
- 第三種情形,若兩個vertex的「搜尋生命週期」完全沒有重疊,那麼這兩個vertex在Depth-First Forest中:
- 有可能在同一棵Depth-First Tree,但是互相沒有「ancestor-descendant」的關係,例如vertex(D)與vertex(C)。此時,
discover[D]\(<\)discover[C],而且finish[D]\(<\)finish[C] - 也有可能在不同棵Depth-First Tree,例如vertex(C)與vertex(H)。此時,
discover[C]\(<\)discover[H],而且finish[C]\(<\)finish[H]。
- 有可能在同一棵Depth-First Tree,但是互相沒有「ancestor-descendant」的關係,例如vertex(D)與vertex(C)。此時,
4種edge

圖六:。
經過DFS()後,還可以分類出四種edge:
- Tree edge:若vertex(Y)是被vertex(X)「發現」,則edge(X,Y)即為Tree edge,也就是Depth-First Tree中的edge。
- 透過顏色判斷edge:當vertex(X)搜尋到vertex(Y),且vertex(Y)為「白色」時,就會建立出Tree edge。
- Back edge:所有指向ancestor的edge,稱為Back edge。如圖六中,edge(F,B)與edge(H,G)。
- 透過顏色判斷edge:當vertex(X)搜尋到vertex(Y),且vertex(Y)為「灰色」,就會建立起Back edge,見圖三(j)、圖三(q)與圖六。
- Forward edge:所有指向descendant但不是Tree edge的edge,稱為Forward edge。觀察「時間軸」,若Graph存在例如:edge(A,D)、edge(A,E)或者edge(B,E),即可稱之為Forward edge。很遺憾的,圖六中,沒有Forward edge。
- 透過顏色判斷edge:當vertex(X)搜尋到vertex(Y)時,vertex(Y)為「黑色」,並且
discover[X]\(<\)discover[Y],edge(X,Y)即為Forward edge。
- 透過顏色判斷edge:當vertex(X)搜尋到vertex(Y)時,vertex(Y)為「黑色」,並且
- Cross edge:若兩個vertex不在同一棵Depth-First Tree上,例如vertex(C)與vertex(H),或者兩個vertex在同一棵Depth-First Tree上卻沒有「ancestor-descendant」的關係,例如vertex(C)與vertex(F),則稱連結此兩個vertex的edge為Cross edge。
- 透過顏色判斷edge:當vertex(X)搜尋到vertex(Y)時,vertex(Y)為「黑色」,並且
discover[X]\(>\)discover[Y],edge(X,Y)即為Cross edge。
- 透過顏色判斷edge:當vertex(X)搜尋到vertex(Y)時,vertex(Y)為「黑色」,並且
分類出四種edge除了可以作為大腦體操,還可以根據Graph中是否具有/不具有某些edge來區分Graph的性質:
- 若在undirected graph上執行一次
DFS(),所有的edge不是Tree edge就是Back edge。 - 若在directed graph上執行一次
DFS(),沒有產生Back edge,則此directed graph必定是acyclic(沒有迴路)。
諸如此類的,是不是很有趣呢?
(好像也還好。)
最後再看一次DFS()的流程,見圖七:

圖七:。
以上便是Depth-First Search(DFS,深度優先搜尋)的介紹。
在接下來的文章中,將利用DFS()與神奇的finish:
- 進行Topological Sort(拓撲排序)。
- 找到directed graph中的Strongly Connected Component(SCC)。
不過在這之前,會先介紹利用BFS()與DFS()找到undirected graph中的connected component作為暖身。
參考資料:
- Introduction to Algorithms, Ch22
- Fundamentals of Data Structures in C++, Ch6
- Code Review:Depth First Search and Breadth First Search in C++
BFS/DFS系列文章
Graph: Breadth-First Search(BFS,廣度優先搜尋)
Graph: Depth-First Search(DFS,深度優先搜尋)
Graph: 利用DFS和BFS尋找Connected Component
Graph: 利用DFS尋找Strongly Connected Component(SCC)
Graph: 利用DFS尋找DAG的Topological Sort(拓撲排序)
回到目錄: