Single-Source Shortest Path：Bellman-Ford Algorithm

Posted by Chiu CC on 3 01, 2016


先備知識與注意事項

本篇文章將介紹Bellman-Ford Algorithm來回應上一篇Single-Source Shortest Path：Intro(簡介)的問題，演算法的概念主要圍繞在：

  • Relaxation
  • Convergence property
  • Path-relaxation property

建議讀者可以先進傳送門精彩回顧一下。

目錄


Graph之表示法(representation)

在BFS/DFS系列文章使用Adjacency List代表Graph，不過edge上沒有weight，可以使用如下資料結構：

  • std::vector<std::list<int>> AdjList;

MST系列文章的Graph利用Adjacency Matrix，因此可以使用如下資料結構，把weight放進矩陣之元素：

  • std::vector<std::vector<int>> AdjMatrix;

本篇文章將利用Adjacency List來代表weighted edge，方法是使用C++標準函式庫(STL)的std::pair<int,int>，使得AdjList的資料結構更新為：

  • std::vector<std::list<std::pair<int,int>>> AdjList;

若有一條從vertex(0)(from)指向vertex(1)(to)的edge(0,1)之weight為\(5\)，若利用新的AdjList表示，如圖一：

  • 將from以std::vector的index表示；
  • 每一個std::pair<int,int>都是一個std::list的node；
  • 將to放在std::pair<int,int>的第一個int資料項；
  • 將weight放在std::pair<int,int>的第二個int資料項，

關於std::pair<int,int>的用法，可以參考：Cplusplus：std::pair。

cc

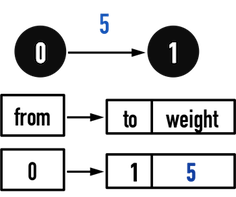
圖一。


Bellman-Ford Algorithm

根據Path-Relaxation Property，考慮一條從vertex(0)到vertex(K)之路徑\(P:v_0-v_1-...-v_K\)，如果在對path之edge進行Relax()的順序中，曾經出現edge(v0,v1)、edge(v1,v2)、...、edge(vK-1,vK)的順序，那麼這條path一定是最短路徑，滿足distance[K]\(=\delta(v_0,v_K)\)。

  • 在對edge(v1,v2)進行Relax()之前，只要已經對edge(v0,v1)進行過Relax()，那麼，不管還有其餘哪一條edge已經進行過Relax()，distance[2]必定會等於\(\delta(0,2)\)，因為Convergence property。

Bellman-Ford Algorihm就用最直覺的方式滿足Path-Relaxation Property：

  • 一共執行\(|V|-1\)次迴圈。
  • 在每一次迴圈裡，對「所有的edge」進行Relax()。
  • 經過\(|V|-1\)次的「所有edge之Relax()」後，必定能夠產生「按照最短路徑上之edge順序的Relax()順序」，也就能夠得到最短路徑。
    • 由於從起點走到任一vertex之最短路徑，最多只會有\(|V|-1\)條edge，因此，執行\(|V|-1\)次迴圈必定能夠滿足「最壞情況」(worst case)。


考慮如圖二(a)之Graph，以vertex(0)作為起點。
並且根據圖二(a)之Adjacency List，得到在Bellman-Ford Algorihm中對所有edge進行Relax()之順序如圖二(b)。

cc

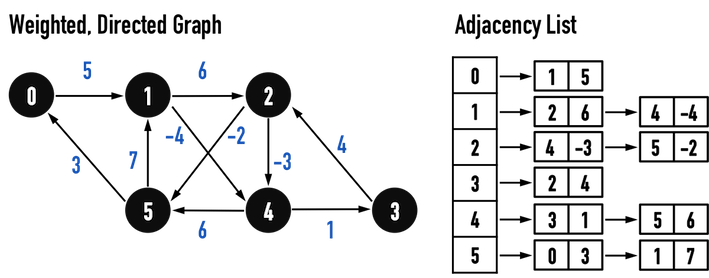
圖二(a)。

cc

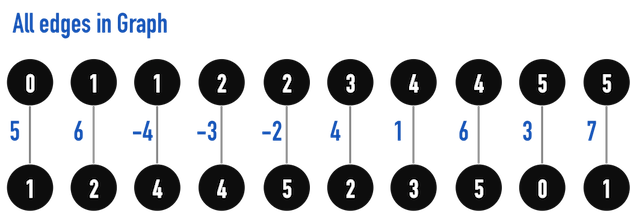
圖二(b)：根據圖二(a)之AdjList，對所有edge進行Relax()之順序。


首先，對Graph的資料項目distance與predecessor進行初始化，見圖二(c)：

  • distance：將起點vertex之distance設為\(0\)，並將其餘vertex之distance設為無限大(\(\infty\))。
    • 如果在演算法結束後，某個vertex之distance仍然無限大(\(\infty\))，則表示Graph中沒有一條path能夠從起點vertex走到該vertex。
    • 回顧Relax()，因為只有起點vertex(0)之distance設為\(0\)，其餘distance都是無限大，因此，在進行「所有edge之Relax()」時，一定是從與起點vertex(0)相連之edge先開始。
  • predecessor：將所有vertex之predecessor設為\(-1\)，表示目前還沒有predecessor。對其餘vertex來說，可以想成還沒有被起點vertex找到。

cc

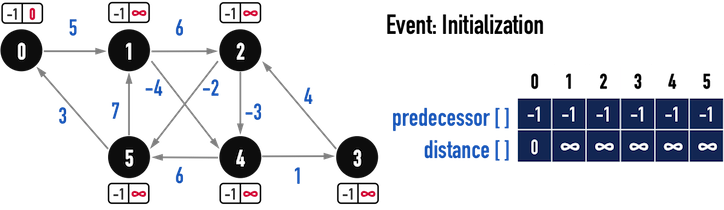
圖二(c)。


接著開始\(|V|-1\)次的迴圈，並在每次迴圈，都對「所有edge」進行Relax()。
(此例，共\(5\)次迴圈，每次按照圖二(b)之順序處理\(10\)條edge)。

第一次迴圈(iteration#1)

對第一條edge(0,1)進行Relax()，見圖三(a)：

  • 比較distance[1]與distance[0]+w(0,1)，發現」從vertex(0)走到vertex(1)」之成本較原先的成本低(原先的成本即為distance[1])，因此更新distance[1]為distance[0]+w(0,1)。
  • 同時更新predecessor[1]=0，表示vertex(1)是從vertex(0)走過去的。

cc

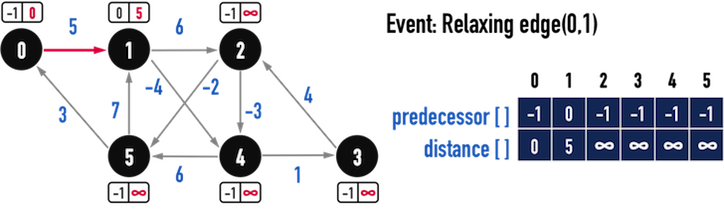
圖三(a)。

對第二、三條edge(1,2)、edge(1,4)進行Relax()，見圖三(b)：

  • 由於distance[2]與distance[4]皆大於從vertex(1)走過去的成本，因此更新：
    • distance[2]=distance[1]+w(1,2)；
    • distance[4]=distance[1]+w(1,4)；

cc

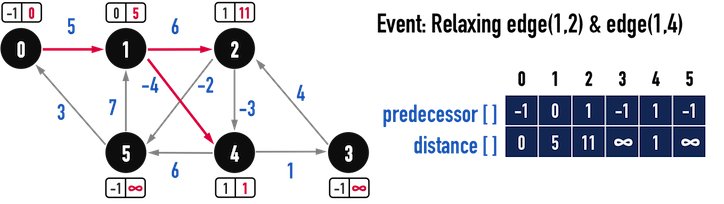
圖三(b)。

對第四、五條edge(2,4)、edge(2,5)進行Relax()，見圖三(c)：

  • 由於distance[4]小於「從vertex(2)走過去的成本(distance[2]+w(2,4))，因此，仍維持從vertex(1)走到vertex(4)之路徑。
  • 而distance[5]大於distance[2]+w(2,5)，因此更新：
    • distance[5]=distance[2]+w(2,5)；
    • predecessor[5]=2；

cc

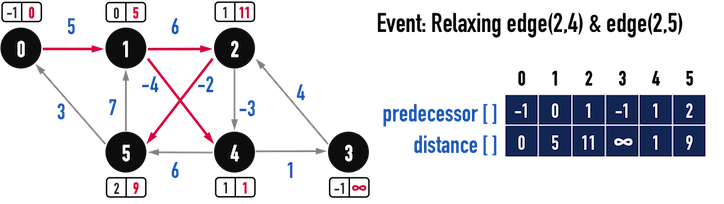
圖三(c)。

對第六條edge(3,2)進行Relax()，見圖三(d)：

  • 顯然，「從vertex(1)走到vertex(2)」之成本distance[2]遠小於「從vertex(3)走到vertex(2)」之成本distance[3]+w(2,3)，因此，不更新抵達vertex(2)之路徑。

cc

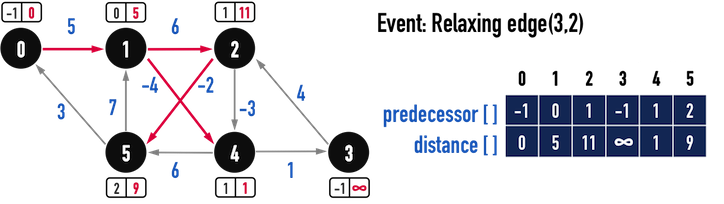
圖三(d)。

對第七、八條edge(4,3)、edge(4,5)進行Relax()，見圖三(e)：

  • 由於distance[3]大於從vertex(4)走到vertex(3)的成本(distance[4]+w(4,3))，因此更新：
    • distance[3]=distance[4]+w(4,3)；
    • predecessor[3]=4；
  • 而且distance[5]也大於distance[4]+w(4,5)，表示「從vertex(4)走到vertex(5)」會比「從vertex(2)走到vertex(5)」還近，便更新：
    • distance[5]=distance[4]+w(4,5)；
    • predecessor[5]=4；

cc

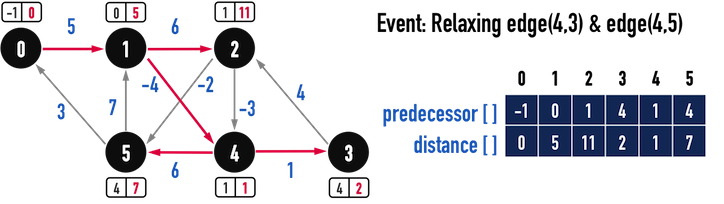
圖三(e)。

對第九、十條edge(5,0)、edge(5,1)進行Relax()，見圖三(f)：

  • 比較distance及edge之weight後發現，從vertex(5)走到vertex(0)與vertex(1)之成本皆高於當前走到此二vertex之路徑，因此不更新。

cc

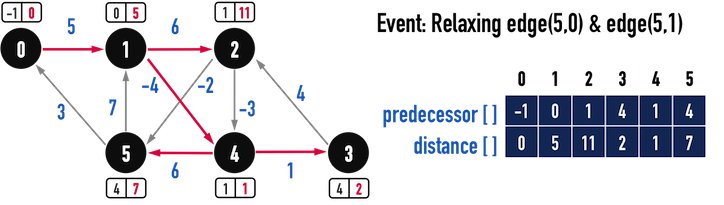
圖三(f)。

經過了第一次迴圈的洗禮，大致能夠掌握Relax()的精髓：如果有比目前的成本更低的路徑，就選擇那條路徑。
例如，圖三(c)中，原本從vertex(0)走到vertex(5)的路徑是\(Path:0-1-2-5\)，但是在圖三(e)時，發現了更短的路徑\(Path:0-1-4-5\)，便更新其成為目前「從vertex(0)走到vertex(5)」的最短路徑。

還有沒有可能更新出成本更低的路徑？

當然有，因為第一次迴圈的Relax()明顯沒有更新到和edge(3,2)有關路徑，其原因在於，Relax()進行的edge順序。
在第一次迴圈中，是先對edge(3,2)進行Relax()，不過此時的distance[3]還是無限大，因此沒有作用，之後才更新出「從vertex(4)走到vertex(3)」的路徑。
就圖三(f)看來，distance[2]為\(11\)，而\(Path:0-1-4-3-2\)之成本只有\(6\)，顯然是低於當前的路徑\(Path:0-1-2\)。

因此需要\(|V|-1\)次迴圈，以確保演算法一定能找到最短路徑。


第二次直到第五次迴圈的邏輯同上，在此就不再贅述。

最後得到的最短路徑之Predecessor Subgraph如圖三(g)：

cc

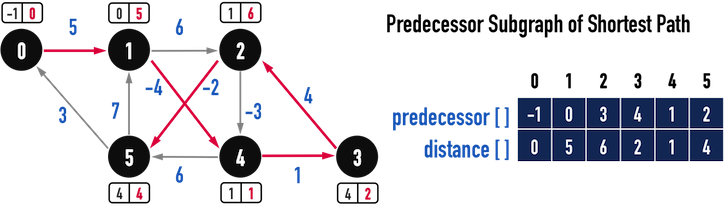
圖三(g)。

根據圖三(g)，從vertex(0)走到Graph中其餘vertex之最短路徑為\(Path:0-1-4-3-2-5\)，若把Bellman-Ford Algorithm中，每一次迴圈對所有edge進行Relax()之順序攤開，如圖三(h)，可以驗證Bellman-Ford Algorithm確實滿足Path-Relaxation Property，按照最短路徑之順序對edge進行Relax()。
(Bellman-Ford Algorithm就是暴力解決，當然會滿足。)

cc

圖三(h)。


程式碼

程式碼包含幾個部分：

class Graph_SP：

  • 使用AdjList，並利用std::pair<int,int>儲存edge的weight。
  • InitializeSingleSource(int Start)：對資料項目distance與predecessor進行初始化，並以int Start作為最短路徑之起點。
  • Relax()：對edge進行Relaxation的主要函式。
  • BellmanFord()：進行Bellman-Ford Algorithm的主要函式，內容如前一小節所述。

以及main()：建立如圖二(a)之AdjList，並進行BellmenFord()。

// C++ code
#include <iostream>
#include <vector>
#include <list>
#include <utility>          // for std::pair<>
#include <iomanip>          // for std::setw()

const int Max_Distance = 100;
class Graph_SP{             // SP serves as Shortest Path
private:
    int num_vertex;
    std::vector<std::list<std::pair<int,int>>> AdjList;
    std::vector<int> predecessor, distance;
public:
    Graph_SP():num_vertex(0){};
    Graph_SP(int n):num_vertex(n){
        AdjList.resize(num_vertex);
    }
    void AddEdge(int from, int to, int weight);
    void PrintDataArray(std::vector<int> array);

    void InitializeSingleSource(int Start);     // 以Start作為起點
    void Relax(int X, int Y, int weight);       // 對edge(X,Y)進行Relax
    bool BellmanFord(int Start = 0);            // 以Start作為起點
                                                // if there is negative cycle, return false
};

bool Graph_SP::BellmanFord(int Start){

    InitializeSingleSource(Start);

    for (int i = 0; i < num_vertex-1; i++) {                // |V-1|次的iteration
        // for each edge belonging to E(G)
        for (int j = 0 ; j < num_vertex; j++) {             // 把AdjList最外層的vector走一遍
            for (std::list<std::pair<int,int> >::iterator itr = AdjList[j].begin();
                 itr != AdjList[j].end(); itr++) {          // 各個vector中, 所有edge走一遍
                Relax(j, (*itr).first, (*itr).second);
            }
        }
    }

    // check if there is negative cycle
    for (int i = 0; i < num_vertex; i++) {
        for (std::list<std::pair<int,int> >::iterator itr = AdjList[i].begin();
             itr != AdjList[i].end(); itr++) {
            if (distance[(*itr).first] > distance[i]+(*itr).second) {   // i是from, *itr是to
                return false;
            }
        }
    }

    // print predecessor[] & distance[]
    std::cout << "predecessor[]:\n";
    PrintDataArray(predecessor);
    std::cout << "distance[]:\n";
    PrintDataArray(distance);

    return true;
}
void Graph_SP::PrintDataArray(std::vector<int> array){
    for (int i = 0; i < num_vertex; i++)
        std::cout << std::setw(4) << i;
    std::cout << std::endl;
    for (int i = 0; i < num_vertex; i++)
        std::cout << std::setw(4) << array[i];
    std::cout << std::endl << std::endl;
}
void Graph_SP::InitializeSingleSource(int Start){

    distance.resize(num_vertex);
    predecessor.resize(num_vertex);

    for (int i = 0; i < num_vertex; i++) {
        distance[i] = Max_Distance;
        predecessor[i] = -1;
    }
    distance[Start] = 0;
}
void Graph_SP::Relax(int from, int to, int weight){

    if (distance[to] > distance[from] + weight) {
        distance[to] = distance[from] + weight;
        predecessor[to] = from;
    }
}
void Graph_SP::AddEdge(int from, int to, int weight){
    AdjList[from].push_back(std::make_pair(to,weight));
}

int main(){

    Graph_SP g7(6);
    g7.AddEdge(0, 1, 5);
    g7.AddEdge(1, 4, -4);g7.AddEdge(1, 2, 6);
    g7.AddEdge(2, 4, -3);g7.AddEdge(2, 5, -2);
    g7.AddEdge(3, 2, 4);
    g7.AddEdge(4, 3, 1);g7.AddEdge(4, 5, 6);
    g7.AddEdge(5, 0, 3);g7.AddEdge(5, 1, 7);

    if (g7.BellmanFord(0))
        std::cout << "There is no negative cycle.\n";
    else
        std::cout << "There is negative cycle.\n";

    return 0;
}

output:

predecessor[]:
   0   1   2   3   4   5
  -1   0   3   4   1   2

distance[]:
   0   1   2   3   4   5
   0   5   6   2   1   4

There is no negative cycle.


檢查Graph中是否存在negative cycle

聰明的讀者一定已經發現了，BellmanFord()還有個功能，可以檢查Graph中是否存在negative cycle。
上一篇文章Single-Source Shortest Path：Intro(簡介)曾經提到，塵世間最痛苦的事情莫過於在處理Single-Source Shortest Path問題時碰上negative cycle，因為negative cycle存在會使得最短路徑出現\(-\infty\)。

若存在從vertex(from)指向vertex(to)的edge(from,to)，並具有weight，根據Relax()的運作原則，：

  • 若distance[to]\(>\)distance[from]+weight，便更新distance[to]=distance[from]+weight」。

因此，在對Graph中所有edge進行Relax()後，所有edge(from,to)所連結的兩個vertex之distance必定滿足：

  • distance[to]\(\leq\)distance[from]+weight

而BellmanFord()的檢查方法，便是在\(|V|-1\)次「對所有edge進行Relax()」後，檢查，若存在任何一條edge(from,to)所連結的兩個vertex之distance關係為：

  • distance[to]\(>\)distance[from]+weight

就表示存在某一條edge之weight永遠可以讓該edge連結之vertex的distance下降，因此Graph中必定存在negative cycle。


以上便是Bellman-Ford Algorithm之介紹。
只要了解：

  • Relaxation
  • Convergence property
  • Path-relaxation property

之概念，即可掌握Bellman-Ford Algorithm的運作邏輯。

下一篇文章將介紹的是，在DAG(directed acyclic graph)中處理Single-Source Shortest Path之演算法。


參考資料：


Shortest Path系列文章

Shortest Path：Intro(簡介)
Single-Source Shortest Path：Bellman-Ford Algorithm
Single-Source Shortest Path：on DAG(directed acyclic graph)
Single-Source Shortest Path：Dijkstra's Algorithm
All-Pairs Shortest Path：Floyd-Warshall Algorithm

回到目錄：

目錄：演算法與資料結構


tags: C++, Graph, Shortest Path, Relaxation,