Shortest Path：Intro(簡介)

先備知識與注意事項

如果非要在這個章節加上一份先備知識，我會說是Google Map。

最短路徑問題(Shortest Path)

為了解決較為廣義的情境，接下來討論的最短路徑問題將考慮的是一個weighted directed graph，以weight總和表示path之成本，並以具有方向性之edge表示兩個vertex之間的關係。

undirected graph的問題能夠以directed graph的模型解決，反之則無法。
不具weight的edge也能夠以weighted edge模擬(將全部weight設為相同數值即可)，反之則無法。
可以視為只能處理unweighted graph之BFS/DFS的擴充包。

定義名詞：

path之weight：若有一條\(Path:0-1-2-...-K\)，定義其weight為所有edge之weight總和，\(w(path)=\sum_{i=1}^{K}w(i-1,i)\)，如圖一。
最短路徑之成本\(w(path)=\delta(X,Y)\)：在Graph上，所有從vertex(X)出發抵達vertex(Y)的path中，具有最小weight之path，稱為最短路徑，其weight滿足：
- \(\delta(X,Y)=\min\){\(w(path)\), for all path from X to Y}。
  (可能有多條path之weight皆為極小值，那麼這些path都是最短路徑。)
若\(\delta(X,Y)=\infty\)，則表示無法從vertex(X)走到vertex(Y)。

圖一。

根據出發的vertex(稱為source)與終點vertex(稱為destination)之數量選擇，可以將最短路徑問題分成四類：

Single-Pair Shortest Path：從單一vertex，抵達某個特定vertex之最短路徑，此為第二種問題的子問題；
Single-Source Shortest Path：從單一vertex，抵達Graph中其餘所有vertex之最短路徑；
Single-Destination Shortest Path：從Graph中的每一個vertex抵達某個特定vertex之最短路徑：
- 此為第二種問題之變形，只要把edge的方向相反，也就是在G^T上，執行第二種問題之演算法即可。
All-Pairs Shortest Path：Graph中的所有vertex抵達其餘所有vertex之最短路徑。
- 若把每一個vertex都當作起點，即可利用第二種問題之方法解決。
- 不過之後將介紹的Floyd-Warshall Algorithm有更好的答案。

綜合以上，先學第二種問題的演算法：以單一vertex為起點，抵達Graph中的其餘所有vertex之最短路徑，再學第四種問題的Floyd-Warshall Algorithm(以及其他高效率的演算法)，就是最明智的選擇。(推銷成功)

先來看個簡單的Single-Source Shortest Path範例：

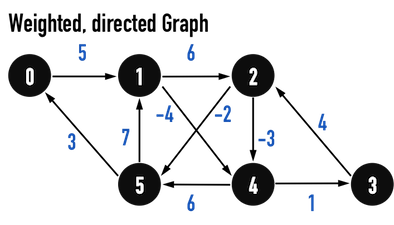
圖二(a)。

如圖二(a)，考慮一個weighted directed graph，若以vertex(0)為起點，要找到從vertex(0)抵達Graph中其餘vertex的最短路徑，結果便如圖二(b)。

考慮從vertex(0)走到vertex(2)：path\(:0-1-2\)的edge數最少，但是weight總和是\(11\)，而edge數較多的\(Path:0-1-4-3-2\)的weight總和只有\(6\)，才是從vertex(0)走到vertex(2)的最短路徑。
原因在於weight有負值(negative value)，所以edge越多的path，weight總和不見得越大(經過某些路徑使得整體成本降低)。

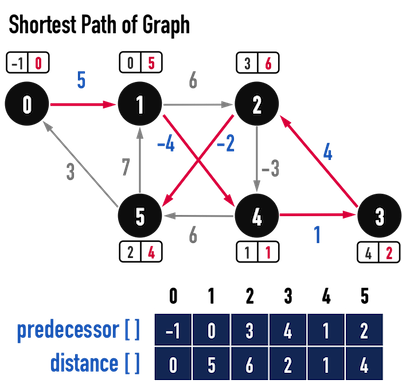
圖二(b)：path上之edge越少，不見得weight總和越小。

如圖二(b)所示，在處理最短路徑問題時，最基本需要用到兩個資料項目：

distance[]：記錄從起點vertex，經過具有weight之edge，走到其餘vertex之「距離」，也就是該條path之weight。若有一條\(Path:0-1-2\)，則path之weight總和即記錄在distance[2]。
predecessor[]：除了距離之外，還希望能夠回溯路徑，因此需要記錄vertex之predecessor，並以此得到Predecessor Subgraph。

由於最短路徑一定不包含cycle，Predecessor Subgraph會是一棵Shortest-Path Tree。

起點vertex即為root；
從root到其餘vertex的path必定是唯一的最短路徑。

(若Graph上出現\(\delta(X,Y)=\infty\)的情況，Predecessor Subgraph會是Shortest-Path Forest。)

限制

為什麼最短路徑一定不包含cycle？

由於weight只要求是實數(real number)，weight可正可負，因此Graph中可能出現weight總和為正的cycle與weight總和為負的cycle。

考慮圖三(a)，cycle\(:1-2-3\)之weight為\(10\)，若path經過此cycle，weight之總和必定會增加，此path不會是最短路徑。考慮從vertex(0)走到vertex(4)：

\(Path:0-1-2-3-4\)之weight為\(10\)；
經過一次cycle，\(Path:0-1-2-3-1-2-3-4\)之weight為\(20\)。

圖三(a)。

考慮圖三(b)，cycle\(:1-2-3\)之weight為\(-6\)，表示path經過此cycle，weight之總和就會減少，而且經過越多次，weight總和越少，所以永遠不會有最短路徑，\(\delta(X,Y)=-\infty\)。考慮從vertex(0)走到vertex(4)：

\(Path:0-1-2-3-4\)之weight為\(4\)；
經過一次cycle，\(Path:0-1-2-3-1-2-3-4\)之weight為\(-2\)；
經過兩次cycle，\(Path:0-1-2-3-1-2-3-1-2-3-4\)之weight為\(-8\)；

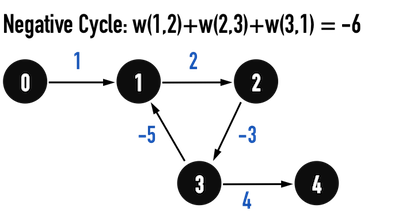
圖三(b)。

因此，在考慮最短路徑問題時，問題之Graph可以有總和為正值的cycle，但是不能有總和為負值的cycle。

而演算法所挑選出來的最短路徑之Predecessor Subgraph，一定不包含cycle。

特徵

最短路徑除了不會有cycle外，還有兩點特徵值得一提。

特徵一：因為最短路徑不存在cycle，在共有\(V\)個vertex之Graph中，從vertex(X)走到vertex(Y)的最短路徑，至多只會包含\(|V|-1\)條edge。

如圖二(b)，從vertex(0)走到vertex(5)的paht上，共有\(5\)條edge。

此種情形發生在Shortest-Path Tree退化成Linked list的時候。

特徵二：。若在Graph上，存在一條從vertex(0)走到vertex(K)的最短路徑，\(P:v_0-v_1-v_2-...-v_K\)，並定義所有path上的vertex所形成的subpath為\(P_{ij}:v_i-v_{i+1}-...-v_j\)，其中\(1\leq i\leq j\leq K\)，那麼每一條subpath都會是最短路徑。
白話文：最短路徑必定是由較小段的最短路徑(subpath)所連結起來的。換句話說，由較小段的最短路徑(subpath)接起來的路徑必定仍然是最短路徑。

圖二(b)中，從vertex(0)走到vertex(5)之最短路徑為：\(P:v_0-v_1-v_4-v_3-v_2-v_5\)，那麼其中的任何一條path，都是兩個vertex之間的最短距離：

從vertex(1)走到vertex(2)之最短路徑：\(P:v_1-v_4-v_3-v_2\)，weight總和為\(1\)。
從vertex(4)走到vertex(5)之最短路徑：\(P:v_4-v_3-v_2-v_5\)，weight總和為\(3\)。

圖二(b)。

以上將「能夠考慮最短路徑問題」的Graph形式，以及「最短路徑之Predecessor Subgraph」的特徵介紹完畢。

接著要介紹尋找最短路徑之演算法核心概念：Relaxation。

觀念：Relaxation

見圖四(a)，現從vertex(S)作為起點，欲尋找抵達vertex(X)與vertex(Y)之最短路徑。

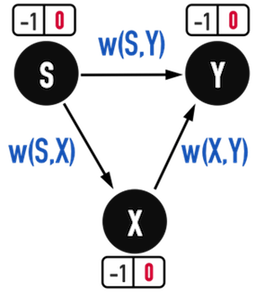
圖四(a)。

其中，vertex(X)之最短路徑只有一種可能，\(\delta(S,X)=w(S,X)\)。
而vertex(Y)可以從vertex(S)或者vertex(X)抵達，因此最短路徑\(\delta(S,Y)\)有兩種可能：

\(\delta(S,Y)=w(S,Y)\)：vertex(Y)經由vertex(S)直接抵達。
\(\delta(S,Y)=w(S,X)+w(X,Y)\)：vertex(S)先經過vertex(X)，再到vertex(Y)。

這兩條path中，weight最小的path即是最短路徑。
找到最短路徑的方法很直觀，只要比較這兩條路徑的weight，挑weight小的path即可。

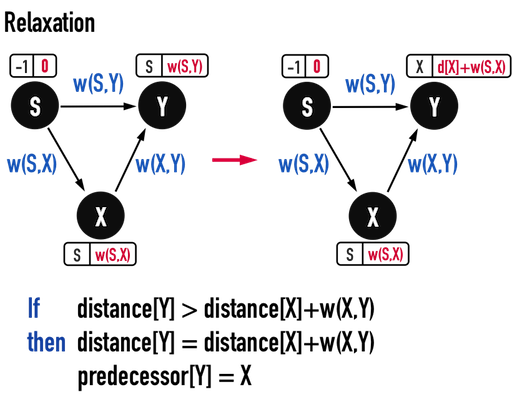
圖四(b)。

以圖四(b)為例，首先從vertex(S)出發，發現其與vertex(X)、vertex(Y)皆有edge相連，便更新兩個vertex的distance為兩條相連edge之weight：

distance[Y]=w(S,Y)；
distance[X]=w(S,X)。

接著考慮經過vertex(X)再到vertex(Y)之path有沒有可能成本較低，便比較distance[Y]與distance[X]+w(X,Y)：

若distance[Y]\(>\)distance[X]+w(X,Y)，則表示\(P:S-X-Y\)之成本小於\(P:S-Y\)，因此從vertex(S)經過vertex(X)再到vertex(Y)才是最短路徑，便更新
- distance[Y]=distance[X]+w(X,Y)；
- predecessor[Y]=X。
反之，若distance[Y]\(<\)distance[X]+w(X,Y)，表示\(P:S-Y\)之成本小於\(P:S-X-Y\)，則不需要更新兩個資料項目，目前的路徑已經是最短路徑。

以上的「比較distance後決定是否更新distance(與predecessor)」步驟，就是Relaxation。

Relax()之範例程式碼如下：

// C++ code
// Relax() as a member function of class Graph_SP

void Graph_SP::Relax(int from, int to, int weight){

    if (distance[to] > distance[from] + weight) {
        distance[to] = distance[from] + weight;
        predecessor[to] = from;
    }
}

根據Relaxation可以衍生出幾個性質：

Triangle inequality

經過Relaxation，並得到最短路徑後，任意兩個在Graph上之vertex(X)與vertex(Y)，若存在edge(X,Y)從vertex(X)指向vertex(Y)，必定滿足以下關係(假設vertex(S)為起點)：

\(\delta(S,Y)\leq \delta(S,X)+w(X,Y)\)。

Upper-Bound property

一旦從vertex(S)抵達vertex(X)之path已經更新至最短路徑\(\delta(S,X)\)，那麼distance[X]將不再更新，保持distance[X]\(=\delta(S,X)\)至演算法程序結束。

觀察Relax()的if條件式，若新的path之weight比原有的path之weight還大，就不更新distance與predecessor。

Convergence property

假定Graph上存在從vertex(X)指向vertex(Y)之edge(X,Y)，並且從起點vertex走到vertex(Y)之最短路徑包含這條edge。
若在對edge(X,Y)進行Relax()之前，從vertex(S)到達vertex(X)的path就已經滿足最短路徑，distance[X]\(=\delta(S,X)\)，那麼在對edge(X,Y)進行Relax()後，必定得到從vertex(S)走到vertex(Y)之最短路徑，並更新distance[Y]\(=\delta(S,Y)\)，而且至此之後，distance[Y]將不會再被更新。

如圖五(a)，\(Path=S-X-Y\)是從vertex(S)走到vertex(Y)的最短路徑，並且在對edge(X,Y)進行Relax()之前，從vertex(S)走到vertex(X)之path已經是最短路徑，distance[X]\(=\delta(S,X)\)，那麼，此時對edge(X,Y)進行Relax()，必定能得到從vertex(S)走到vertex(Y)之最短路徑，distance[Y]\(=\delta(S,Y)\)。

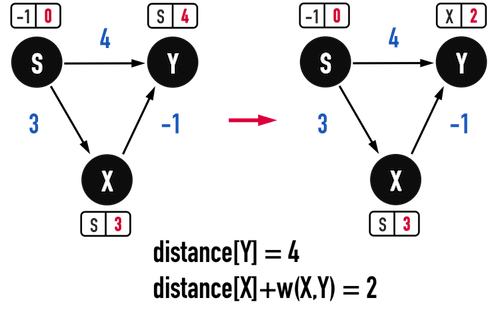
圖五(a)。

但是若從vertex(S)走到vertex(Y)之最短路徑不包含edge(X,Y)，那麼即使在對edge(X,Y)做Relax()之前，distance[X]已經等於\(\delta(S,X)\)，distance[Y]仍然不更新。

這表示，distance[Y]已經等於\(\delta(S,Y)\)，如圖五(b)。或者，從vertex(S)走到vertex(Y)之最短路徑會從其他vertex走到vertex(Y)。

圖五(b)。

Path-relaxation property

考慮一條從vertex(0)到vertex(K)之路徑\(P:v_0-v_1-...-v_K\)，如果在對path之edge進行Relax()的順序中，曾經出現edge(v₀,v₁)、edge(v₁,v₂)、...、edge(v_K-1,v_K)的順序，那麼這條path一定是最短路徑，滿足distance[K]\(=\delta(v_0,v_K)\)。

在對edge(v₁,v₂)進行Relax()之前，只要已經對edge(v₀,v₁)進行過Relax()，那麼，不管還有對其餘哪一條edge進行Relax()，distance[2]必定會等於\(\delta(0,2)\)，因為Convergence property。

例如，現有一條從vertex(0)走到vertex(3)之最短路徑為\(Path:0-1-2-3\)，根據Convergence property，只要在對edge(1,2)進行Relax()之前，已經對edge(0,1)進行Relax()，如此便保證\(Path:0-1-2\)一定是最短路徑，此時再對edge(2,3)進行Relax()，便能找到\(Path:0-1-2-3\)。
換言之，只要確保Relax()的過程曾經出現「edge(0,1)->edge(1,2)->edge(2,3)」的順序，不需理會中間是否有其他edge進行Relax()，即使有也不影響最後結果。

例如，Relax()順序：「edge(2,3)->edge(0,1)->edge(2,3)->edge(1,2)->edge(2,3)」仍可以得到最短路徑，distance[3]\(=\delta(0,3)\)。

精彩預告

接下來三篇文章，將介紹處理Single-Source Shortest Path的三種演算法，各別的適用情境與時間複雜度如下：
(注意：一律不允許negative cycle出現)

Bellmem-Ford Algorithm：
- 只要Graph中沒有negative cycle，即使有positive cycle、edge有negative weight，皆可使用。
- 時間複雜度：\(O(VE)\)。
Shortest Path on DAG：
- 只要Graph中沒有cycle，即使edge有negative weight，亦可使用。
- 時間複雜度：\(O(V+E)\)。
Dijkstra's Algorithm：
- 只要Graph中的edge沒有negative weight，即使有cycle，亦可使用。
- 時間複雜度，根據實現Min-Priority Queue之資料結構將有所不同：
  - 若使用普通矩陣(array)，需要\(O(E+V^2)\)；
  - 若使用Binary Heap，需要\(O((E+V)\log V)\)；
  - 若使用Fibonacci Heap，只需要\(O(E+V\log V)\)。

將以上描述做成表格，見表一與表二：

	有positive cycle	沒有positive cycle
有negative weight	Bellman-Ford	on DAG
沒有negative weight	Dijkstra	All three

表一：三種演算法之使用情境比較

Bellman-Ford	on DAG	Dijkstra(worst)	Dijkstra(best)
\(O(VE)\)	\(O(V+E)\)	\(O(E+V^2)\)	\(O(E+V\log V)\)

表二：三種演算法之時間複雜度比較

參考資料：

Shortest Path系列文章

Shortest Path：Intro(簡介)
Single-Source Shortest Path：Bellman-Ford Algorithm
Single-Source Shortest Path：on DAG(directed acyclic graph)
Single-Source Shortest Path：Dijkstra's Algorithm
All-Pairs Shortest Path：Floyd-Warshall Algorithm

回到目錄：

目錄：演算法與資料結構