Tree(樹): Intro(簡介)

Posted by Chiu CC on 12 19, 2015


先備知識與注意事項

若熟悉Linked List(連結串列)將會更容易理解樹：Linked list是一維的線性結構(不是往前、就是往後)，樹(與Graph)則推廣成多維的結構。

linkedlist

圖一：A、B、C、D稱為node(節點)，用以代表資料(data)、狀態(state)。
連結各個node之間的連結(link)稱為edge，可能是單方向，或者雙向。

關於Linked list，請參考：

OK Go.

目錄


隨處可見的Tree(樹)

Tree(樹)是用以描述具有階層結構(hierarchical structure)的問題的首選，階層結構意味著明確的先後次序，例如，若要印出ABC三個字母的所有排列組合(permutation)，直覺反射的圖像會是：


fig1.a              fig1.b

圖二：ABC字母排列組合。
視R為樹根(root)，每一個選擇狀態視為node，此即為樹的結構。


圖二的邏輯為：從起點(R)開始，先決定第一個字母，再依序決定第二、第三個字母，並且，在每一次選擇字母時，可能有不止一個可供選擇的字母。最後一共走出六條路徑，得到六種排列組合，而且這六種排列方式只能經由一種唯一的選擇方式(唯一的路徑)產生。
若將起點(R)視為樹根(root)，每一個字母選擇的狀態(例如：A、C、BC、CAB)都視為一個node，這樣的結構便能夠視為一棵樹。

另外如一本書的目錄、族譜、企業的職位關係，甚至是更廣義的「從家門口為起點尋找方圓一公里以內的便利商店」都能夠建立出樹的模型。


那麼，樹最根本的特徵是什麼？

以族譜為例，若定義包龍星是宋世傑的爸爸，那麼包龍星就絕對不能同時又是宋世傑的兒子。

圖三以node與edge描述此關係，並定義箭頭是從父指向子，則：

  • 包龍星指向宋世傑的箭頭表示包為父、宋為子；
  • 宋世傑指向包龍星的箭頭表示宋為父、包為子；

後者的箭頭即違反了最初「包龍星是宋世傑的爸爸」的命題，此即稱為cycle，也就是著名的「雞生蛋」與「蛋生雞」。

cycle

圖三：包龍星若是宋世傑的parent(父)，又同時為其child(子)，即形成cycle。

而樹的最根本特徵就是：在樹的結構裡，只有一個root(樹根)，並且不存在cycle。
此特徵將衍生出另外兩項等價的性質：

  1. 在樹中若要從root尋找特定node，一定只存在一條路徑(path)。
  2. 每個node只會有一個parent。


還有哪些結構是樹？

下列四種結構中，a、b可以視為樹，而c、d則否：

fig2.a

圖三.a：若樹的node只有指向left subtree(左子樹)與right subtree(右子樹)時，又稱為Binary Tree(二元樹)。

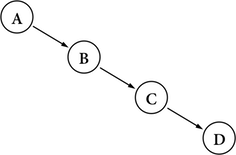
fig2.b

圖三.b：若樹退化成Linked list(連結串列)，仍滿足樹的定義。

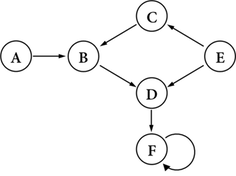
fig2.c

圖三.c：在F出現cycle；以及，D有兩個parent node。

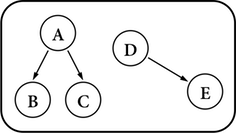
fig2.d

圖三.d：一棵樹只能有一個root(樹根)。此圖像又稱為Forest(樹林)。


用以描述一棵樹的元素

配合圖四，以下將介紹在樹中常見的元素。

針對node / vertex：

  • degree(分歧度)：一個node擁有的subtree(子樹)的個數。
    • 圖四，A的degree為\(3\)，F的degree為\(2\)，N的degree為\(0\)。
  • root(樹根)：樹中最上層的node，也是唯一一個其parent為NULL的node。
    • 圖四，A即為root。
  • leaf：沒有child/subtree的node稱為leaf node。
    • 圖四，G、H、J、K、L、M、N皆為leaf node。
  • external node：沒有child的node。因此，leaf node與external node同義。
  • internal node：至少有一個child的node，稱為internal node。
    • 圖四，A、B、C、D、E、F、I皆為internal node。

fig3

圖四：這是一棵普通的樹。

針對樹：

  • parent <--> child：以pointer說明，被指向者(pointed)為child，指向者(point to)為parent。
    • 圖四，A為C的parent，C為A的child；E為K的parent，K為E的child。
  • siblings：擁有相同parent的node們，互相稱兄道弟。
    • 圖四，B、C、D共同的parent為A，那麼B、C、D即為彼此的sibling。
  • descendant(子嗣)：圖四中，站在A，所有能夠以「parent指向child」的方式找到的node，皆稱為A的descendant，因此整棵樹除了A以外皆為A的descendant。
    • 站在F，能夠以「parent指向child」找到的node有L、M，則稱L、M為F的descendant。
  • ancestor(祖先)：圖四中，站在K，所有能夠以「尋找parent」的方式找到的node，皆稱為K的ancestor，因此，E、B、A皆為K的ancestor。
  • path(路徑)：由descendant與ancestor關係連結成的edge，例如A-B-E-K、A-C-F-N。
  • level：定義root的level為\(1\)，其餘node的level為其parent的level加一。
  • height of node：某一node與其最長path上之descendant leaf node之間的edge數。
    • 例如，F的height為\(1\)，D的height為\(2\)，leaf node的height為\(0\)。
  • height of tree：樹的height即為root的height。
    • 圖四中，樹的height為A的height，等於\(3\)。
  • depth：某一node與root之間的edge數。
    • 例如，F的depth為\(2\)，L的depth為\(3\)。

可以想像的是，在樹中的traversal(尋訪)之時間複雜度(time complexity)會與height(樹高)有關。


定義

以下列出兩種互相等價的Tree(樹)的定義：

A. Tree(樹)是由一個或多個節點所組成的有限集合，並且滿足：

  1. 存在且只有一個稱為root(樹根)的節點；
  2. 其餘的節點可以分割成任意正整數個(包含零個)互斥(disjoint)的集合：\(T_1、...、T_n\)，其中每一個集合也都滿足樹的定義，這些集合又稱為這棵樹的subtree(子樹)。

B. Tree(樹)是由一個或多個nodes/vertices以及edge所組成，而且沒有cycle的集合(set)。

在圖三(d)中，曾出現Forest(樹林)，其定義也很直觀：

  • 由\(n\geq 0\)棵彼此互斥(disjoint)的Tree(樹)所形成的集合(Set)，即稱為Forest(樹林)。

forest

圖五：Forest(樹林)由多個Tree(樹)所組成，可以用來表示互斥集合(disjoint set)。


程式碼

實務上，要以程式碼實作一棵樹，常用的手法為：先以class TreeNode(或是struct)定義出每顆node能夠指向多少subtree、攜帶哪些資料形態，再以另一個class Tree表示整棵樹，並以root作為樹的存取點：

// C++ code
class Tree;
class TreeNode{
    TreeNode *leftchild;   // 以下表示每一個node有四個pointer指向child
    TreeNode *rightchild;
    TreeNode *whatever;
    TreeNode *works;
    int data1;             // node所攜帶的information
    double data2;
    ...
    friend class Tree;     // 讓class Tree能夠存取TreeNode的private data
};
class Tree{
    TreeNode *root;        // 以root作為存取整棵樹的起點
};


集合關係

Tree(樹)位居承先啟後的重要戰略位置，圖六是常見的與Tree有關的資料結構之集合關係圖：

fig4

圖六：與Tree(樹)相關的資料結構之集合關係。

本篇介紹的Tree(樹)並沒有限制child/ subtree的個數，理論上可以有多到超過記憶體空間的child node。

然而在實務上，較常使用每個node至多只有兩個child的樹，稱為Binary Tree(二元樹)。

從Binary Tree再增加「鍵值(Key)大小規則」，即得到Binary Search Tree(BST，二元搜尋樹)。

以BST為基礎，在每個node上添加顏色(紅與黑)用以平衡樹的height，以減短搜尋時間，這種樹稱為Red Black Tree(RBT，紅黑樹)。

另一個方向，若打破「不能存在cycle」的限制，則從Tree推廣至圖(Graph)。

在接下來的文章將先以縮小集合的方向依序介紹：Binary Tree、BST、RBT，再進入Graph(圖)這個更複雜的主題。


參考資料：


Tree系列文章

Tree(樹): Intro(簡介)
Binary Tree: Intro(簡介)
Binary Tree: Traversal(尋訪)
Binary Tree: 建立一棵Binary Tree
Binary Search Tree: Intro(簡介)
Binary Search Tree: Search(搜尋資料)、Insert(新增資料)
Binary Search Tree: Sort(排序)、Delete(刪除資料)
Red Black Tree: Intro(簡介)
Red Black Tree: Rotation(旋轉)
Red Black Tree: Insert(新增資料)與Fixup(修正)
Red Black Tree: Delete(刪除資料)與Fixup(修正)

回到目錄：

目錄：演算法與資料結構


tags: C++, Intro,