Red Black Tree: Rotation(旋轉)

先備知識與注意事項

雖說是Rotation(旋轉)，但其實沒有這麼神奇，只是視覺上看起來像旋轉，在電腦實際將讀取的程式碼實現上，僅僅是數個pointer之指向的重新改寫，所以千萬別害怕。

本篇文章的第一部分將以Insert(新增資料)與Delete(刪除資料)來說明為什麼需要Rotation(旋轉)，但是讀者可以先不必理會細節，因為實際上的Insert與Delete將有更多情況必須考慮，此部分將留待後續文章逐項說明，在本篇文章只要掌握Rotation(旋轉)即可。

於RBT中進行Insert與Delete後竟然不符合RBT

現考慮如圖一(a)之RBT，欲進行Insert(新增資料)與Delete(刪除資料)：

圖一(a)：一棵符合規則的RBT。

為滿足RBT之特徵第五點：從root走向任何一個leaf node(NIL)的任何一條path上之黑色node數皆相同，一般在RBT中Insert(新增資料)時，會先將欲新增的node塗成紅色。
若幸運地，新增的node接在黑色node上，則RBT仍然是一棵RBT，如圖一(b)，新增node(15)。

圖一(b)：在RBT中新增node(15)，新增完後仍然滿足RBT之規則。

但是，若要在RBT中新增node(31)，因為node(34)是紅色，此處便會出現紅色與紅色相連的情況，違反RBT之第四點特徵，因此需要修正，如圖一(c)。

圖一(c)：在RBT中新增node(31)，新增完後無法滿足RBT之規則。

修正的方法便是將node(35)塗成紅色，node(34)塗成黑色，並且對node(35)進行Right Rotation(向右旋轉)，如此一來，RBT便能維持其基本特徵。
值得注意的是，在執行Rotation時，有時會順便調整RBT的height(樹高)，使得RBT維持在平衡(balanced)的狀態。

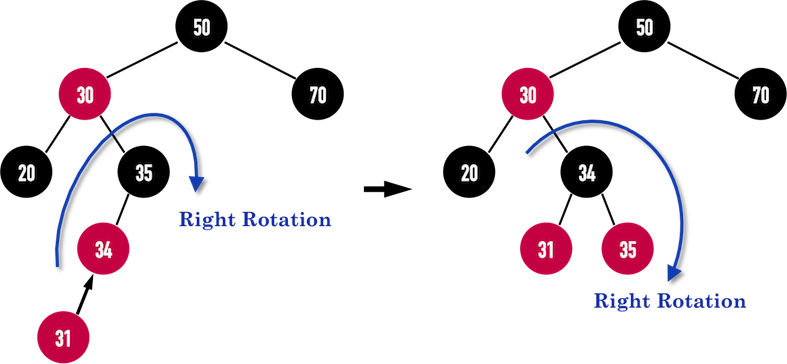
圖一(d)：使用Rotation對Insert(新增資料)進行修正。

在正確新增node(31)後，若要刪除node(20)，因為node(20)是黑色，若將其刪除則違反RBT之第五點特徵：從root走向任何一個leaf node(NIL)的任何一條path上之黑色node數皆相同，因此同樣需要進行修正。

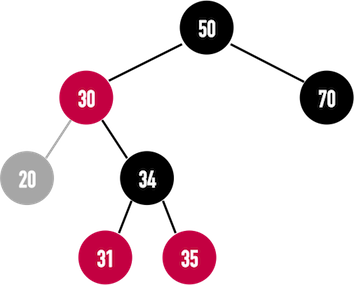
圖一(e)：因為node(20)是黑色，若將其刪除會違反RBT之第五點特徵。

修正的方法則是將node(30)塗黑，node(34)塗紅，然後對node(34)進行Left Rotation(向左旋轉)，如此一來，RBT便能維持其基本特徵。

圖一(f)：使用Rotation對Delete(刪除資料)進行修正。

經過以上說明，應該能體會到Rotation在修正Insert(新增資料)與Delete(刪除資料)時的威力，接著便來實地走訪Rotation實際上是哪些pointer在指來指去。

Rotation(旋轉)

在說明Rotation(旋轉)之前有兩點需要先申明：

若是要應用在BST上，則Rotation(旋轉)前後的BST必須要維持相同之Key排序。此處介紹的Rotation(旋轉)便屬於此類。
Rotation(旋轉)與node是否具有顏色無關，即使是在一般的BST，亦能夠使用Rotation(旋轉)來調整height(樹高)。

Left Roration(向左旋轉)

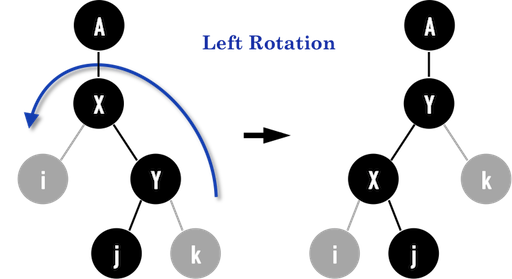
圖二(a)：。

從圖二(a)中可以看出，要對以node(X)為root之subtree進行Left Rotation，必須調整的pointer分別長在node(X)、node(Y)、node(A)與node(j)身上，其中node(j)有可能為NIL，不過為求完整，在此將以node(j)不為NIL作說明。

另外，node(i)與node(k)是否為NIL皆不影響Left Rotation。

由圖二(a)看得出來，node(i)在旋轉前後始終是node(X)的left child；
node(k)在旋轉前後始終是node(Y)的right child。

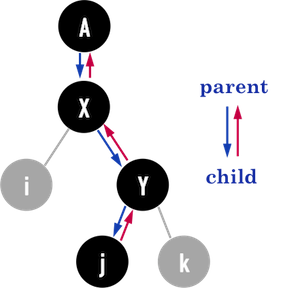
圖二(b)：。

圖二(b)將所有可能需要更動的pointer列出，其中，藍色箭頭表示「由parent指向child」，紅色箭頭則為「child指向parent」。

Left Roration(向左旋轉)之步驟如下：

在Left Rotation完成後，node(Y)的leftchild將會接上node(X)，因此要先把原先node(Y)的leftchild(也就是node(j))放到node(X)的rightchild：
- 圖二(c)左：將node(X)的rightchild指向node(j)；
- 圖二(c)右：將node(j)的parent指向node(X)。

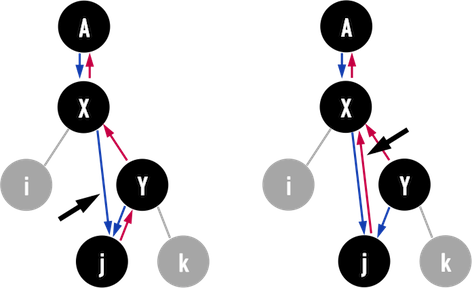
圖二(c)：。

Left Rotation完成後，node(X)的parent將會是node(Y)，而node(Y)的parent要改成原先node(X)的parent(也就是node(A))：
- 圖二(d)左：將node(Y)的parent指向node(A)。
- 圖二(d)右：接著判斷，若原先node(X)是node(A)的leftchild，那麼node(Y)同樣是node(A)的leftchild，反之，node(Y)則成為node(A)的rightchild。

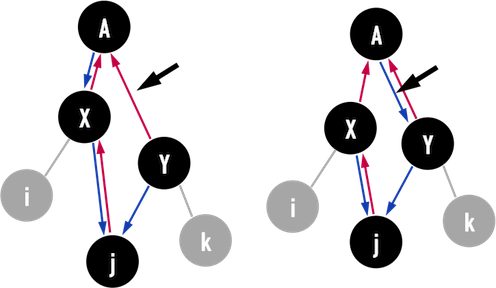
圖二(d)：。

最後，只要再把node(Y)的leftchild指向node(X)，如圖二(e)左，並把node(X)的parent接上node(Y)，如圖二(e)右，Left Rotation便完成了。

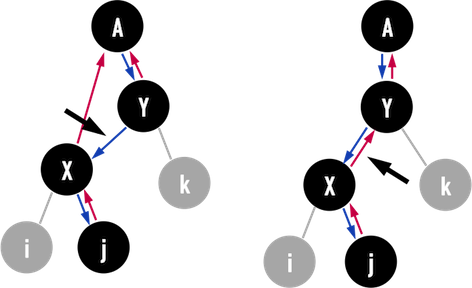
圖二(e)：。

最後再看一次圖二(a)，若忽略node(A)，左圖中，其餘node之Key順序為\(i<X<j<Y<k\)，而右圖中的順序亦為\(i<X<j<Y<k\)，因此，如上所述的Left Rotation能夠應用在BST上。

圖二(a)：。

Left Rotation之程式範例如下：

// C++ code
void RBT::LeftRotation(TreeNode *x){

    TreeNode *y = x->rightchild;         // 把y指向x的rightchild, 最後y會變成x的parent

    x->rightchild = y->leftchild;        // 圖二(c)左, 把y的leftchild托在x的rightchild

    if (y->leftchild != neel){           // 圖二(c)右, 若node(j)為NIL則忽略
        y->leftchild->parent = x;        // 將原先y的leftchild的parent改成x
    }

    y->parent = x->parent;               // 圖二(d)左, 更新y的parent

    if (x->parent == neel){              // 圖二(d)右, 若原先x是root, 旋轉後y變成新的root
        root = y;          
    }         
    else if (x == x->parent->leftchild){ // 若原先x是其parent的leftchild
        x->parent->leftchild = y;        // 更新後y也是其parent的leftchild
    }
    else{                                // 若原先x是其parent的rightchild
        x->parent->rightchild = y;       // 更新後y也是其parent的rightchild
    }
    y->leftchild = x;                    // 圖二(e)左, 最後才修改y與x
    x->parent = y;                       // 圖二(e)右
}

Right Roration(向左旋轉)

Right Rotation的邏輯與Left Rotation完全相同，只要確實地把與node(X)、node(Y)、node(A)與node(j)有關的pointer重新指向正確的記憶體位置，就能夠完成Right Rotation。

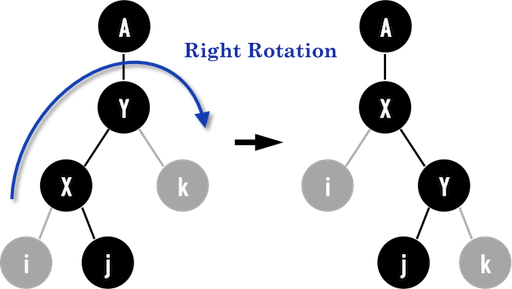
圖三：。

Right Rotation之程式範例如下，把所有LeftRotation()中的left-與right-對調就是了：

// C++ code
void RBT::RightRotation(TreeNode *y){

    TreeNode *x = y->leftchild;           // 把x設成y的leftchild

    y->leftchild = x->rightchild;         // 把x的rightchild放到y的leftchild    
    if (x->rightchild != neel){           // 若x的rightchild不為NIL, 將其parent指向y
        x->rightchild->parent = y;
    }
    x->parent = y->parent;                // 將x的parent指向原先y的parent
                                          // 以下一組if-else將修改原先y的parent之child
    if (y->parent == neel){               // 若y原先是root, x將成為新的root
        root = x;          
    }              
    else if (y == y->parent->leftchild){  // 若原先y是其parent之leftchild, 
        y->parent->leftchild = x;         // x就成為其新的parent之leftchild
    }
    else{                                 // 若原先y是其parent之rightchild, 
        y->parent->rightchild = x;        // x就成為其新的parent之rightchild
    }
    x->rightchild = y;                    // 將y設為x之rightchild
    y->parent = x;                        // 將x設為y之parent
}

以上便是Rotation(旋轉)的說明，在接下來介紹Insert(新增資料)與Delete(刪除資料)的兩篇文章中將會再次與各位相會。

參考資料：

RBT系列文章

Red Black Tree: Intro(簡介)
Red Black Tree: Rotation(旋轉)
Red Black Tree: Insert(新增資料)與Fixup(修正)
Red Black Tree: Delete(刪除資料)與Fixup(修正)

回到目錄：

目錄：演算法與資料結構