先備知識與注意事項*
(完整範例程式碼也可以看這裡:RBT_Insert_Delete.cpp)
RBT也是一棵BST,而RBT之Insert(新增資料)方法便是先沿用InsertBST(),再對顏色進行修正。而修正的方法將用上Rotation(),因此,建議在閱讀本篇文章之前,先熟悉Binary Search Tree: Search(搜尋資料)、Insert(新增資料)與Red Black Tree: Rotation(旋轉)會很有幫助。
目錄
如同於BST中Insert(新增資料)
RBT也是一棵BST,在Insert(新增資料)時,必須滿足:Key(L)<Key(Current)<Key(R),因此,RBT的InsertRBT()前半部演算法與BST的函式:InsertBST()大同小異。
需要修改/擴充的部分有三處:
NIL:所有原先在BST中指向NULL的pointer,在RBT中需要修正成指向NIL,包括「條件式」與「新增node的child pointer」。- 顏色:如同在RBT:Rotation(旋轉)所說,一般預設新增node為紅色,因此,若新增node接在黑色node之後,仍能滿足RBT的特徵。但是若新增node接在紅色node之後,則違反了RBT之第四點特徵,必須進行修正。
- 引進函式:
InsertFixedUpRBT()進行修正。
InsertRBT()的程式範例如下:
// C++ code
void RBT::InsertRBT(int key, string str){
// 前半部與 InsertBST()之邏輯完全相同, 僅僅需要修改 NULL <-> NIL
TreeNode *y = neel;
TreeNode *x = root;
TreeNode *insert_node = new TreeNode(key, str);
while (x != neel) { // 把root初始化成neel, 這裡就可以用neel來做判斷
y = x;
if (insert_node->key < x->key){
x = x->leftchild;
}
else{
x = x->rightchild;
}
}
insert_node->parent = y;
if (y == neel){
this->root = insert_node;
}
else if (insert_node->key < y->key){
y->leftchild = insert_node;
}
else{
y->rightchild = insert_node;
}
// 以下是對RBT之node的設定, 將child pointer指向NIL, 顏色設為紅色
insert_node->leftchild = neel;
insert_node->rightchild = neel;
insert_node->color = 0; // 顏色可以在constructor中預設
InsertFixedUpRBT(insert_node); // 對可能出現紅色與紅色node相連之情形做修正
}
修正:InsertFixUpRBT()
什麼情況需要對InsertRBT()做修正?
當新增node接在紅色的node的child pointer,形成紅色與紅色相連時。
考慮以下情況,如圖一(a),新增的node將要接在node(X)上:
- node(X)為其
parent,顏色為紅色; - node(Y)為其
uncle,其顏色可能為紅色或黑色。 - node(Z)為其grandparent,顏色必定為黑色(因為node(X)是紅色);
- node(W)的顏色可能是紅色或黑色。
- 所有灰色node(如node(a)、node(b)、node(c)、node(d))表示:只要不影響RBT之特徵,其顏色、是否實際攜帶資料或是否為
NIL並不影響結果。

圖一(a):。
根據uncle的顏色是紅色或者黑色,可以將修正(FixUp)分成三種情形(case):
- Case1:
uncle是紅色,不論新增的node是node(X)的leftchild或rightchild; - Case2:
uncle是黑色,而且新增的node為node(X)的rightchild; - Case3:
uncle是黑色,而且新增的node為node(X)的leftchild。
Case1
圖一(b)左,此時current指向新增的node(A),而node(A)成為node(X)的rightchild,其uncle:node(Y)是紅色的。
修正的方法就是「把債還給上一代的上一代」:
- 將
parent塗成黑色:node(X)塗成黑色; - 將
uncle塗成黑色:node(Y)塗成黑色; - 將
parent->parent塗成紅色:node(Z)塗成紅色: - 將
current從node(A)移到node(Z)。
此時,如圖一(b)右,從node(Z)出發往其descendant leaves的任一path上之黑色node數皆相同,這個subtree便滿足了RBT的特徵。

圖一(b):。
接著必需根據node(W)的顏色採取不同行動:
- 若node(W)為黑色,就不需要再做調整;
- 若node(W)為紅色,則node(Z)與node(W)再次形成紅色node與紅色node相連,必須重複同樣的判斷流程。
若node(A)成為node(X)的leftchild,如圖一(c),修正的方法同上。

圖一(c):。
Case3
圖一(d),新增的node(A)成為node(X)的leftchild,其uncle:node(Y)是黑色。

圖一(d):。
事實上,若current指向之node(此為node(A))是新增的node,則根據RBT之第五點特徵,其uncle:node(Y)必定是NIL,如圖一(e)左。
不過,在稍後的範例中將會看到,current不一定是「剛剛新增的node」,也有可能是「修正到一半,出現紅色與紅色相連的node」,但因為是「修正到一半」,尚未調整node(Z)的顏色,因此所有從node(Z)往其descendant leaves的任意path上之黑色node數必定不變,此時,若node(Y)不為NIL,則node(X)以及node(A)必定還有黑色的child pointer,如圖一(e)右所示,node(a)、node(b)與node(c)皆為黑色。

圖一(e):。
修正方法如下,見圖一(f):
- 將
parent塗成黑色:node(X)塗成黑色; - 將
parent->parent塗成紅色:node(Z)塗成紅色; - 對
parent->parentnode(Z)進行Right Rotation(向右旋轉)。

圖一(f):。
經過Case3的修正,必定會滿足RBT之規則,原因在於:
- 先考慮圖一(e),若從node(A)往其descendant leaves的任意path上之黑色node數為\(M\),則從node(Z)往其descendant leaves的任意path上之黑色node數為\(M+1\);
- 再看圖一(g),因為在修正的過程中,node(Z)從黑色被修改成紅色,因此從node(Z)往其descendant leaves的任意path上之黑色node數下修為\(M\),與node(A)相同,使得整棵樹滿足RBT之特徵。

圖一(g):。
Case2
圖一(h),新增的node(A)成為node(X)的rightchild,其uncle:node(Y)是黑色。

圖一(h):。
如同Case3,圖一(h)的uncle:node(Y)同樣有兩種可能:攜帶實際資料的黑色node,或者NIL,如圖一(i):

圖一(i):。
而修正Case2的方法就是將其轉換成Case3,再利用上述Case3的方法調整成正確的RBT。
從Case2調整成Case3,如圖一(j):
- 將
current移至current->parent:將current從node(A)移到node(X); - 對新的
current進行Left Rotation:對node(X)進行Left Rotation。
圖一(j)右符合Case3:「current成為其parent的leftchild,且其unclenode(Y)是黑色」,因此,只要再進行如同圖一(f)之修正流程即可。

圖一(j):。
幾個範例
Example1
考慮一棵RBT如圖二(a):

圖二(a):。
若想新增node(75),由於其將接在node(80)的leftchild位置上,而node(80)為紅色,因此需要進行修正。
接著觀察,node(75)之uncle:node(60),是紅色,因此可以使用Case1的方法修正,如圖二(b):
- 將
parent與uncle塗黑:node(80)與node(60)塗黑; - 將grandparent塗紅:node(70)塗紅;
- 將
current移至node(70); - 進入下一個迴圈判斷node(70)是否與其
parent形成紅色與紅色node相連。
恰好,node(50)為root,一定是黑色,因此新增node(75)便算是完成。

圖二(b):。
若想繼續新增node(25),由於其將接在node(30)的leftchild,而node(30)為紅色,因此需要修正。
接著觀察,node(25)之uncle為NIL是黑色,而node(25)本身是leftchild,因此可以使用Case3的方法,如圖二(c):
- 將
parent塗成黑色:node(30)塗成黑色; - 將
parent->parent塗成紅色:node(40)塗成紅色; - 對
parent->parent:node(40)進行Right Rotation(向右旋轉)。

圖二(c):。
若想繼續新增node(79),由於其將接在node(75)的rightchild,而node(75)為紅色,因此需要修正。
接著觀察,node(79)之uncle為NIL是黑色,而node(79)本身是rightchild,因此可以使用Case2的方法,先將問題從Case2轉換成Case3,再由Case3之方法修正,如圖二(d):

圖二(d):。
Example2
考慮一棵RBT如圖三(a):

圖三(a):。
要在其中新增node(4),則會依序經歷case1、case2直到case3完成修正,如圖三(b)、圖三(c)、圖三(d)與圖三(e)所示。

圖三(b):。
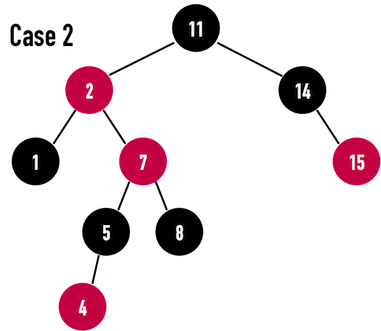
圖三(c):。
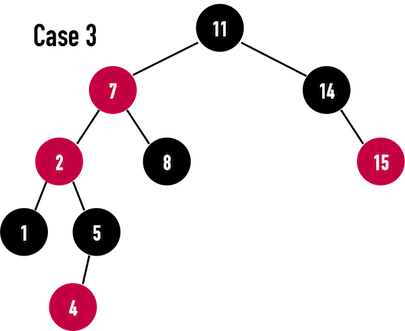
圖三(d):。
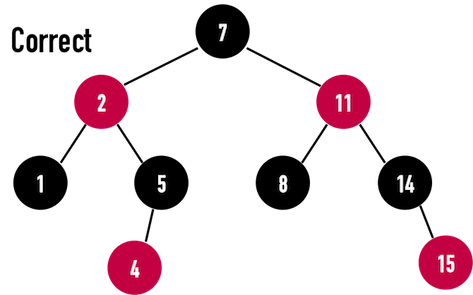
圖三(e):。
根據以上說明,可以歸納出對於InsertRBT()的修正(Fix-Up)之情形(Case)間的循環圖,如圖四:
- 當新增node之
parent為紅色時,需要對RBT進行修正; - 若進入Case1,有可能執行一次即完成,也有可能再次出現紅色與紅色相連的情況,如圖三(b)-(c);
- 若進入Case2,就轉換成Case3的情境;
- 一旦進入Case3,經過修正後必定能滿足RBT之特徵限制。

圖四:。
最後還有一點需要說明。
圖五中:
- 左圖是本篇文章介紹修正(Fix-Up)的出發點:將新增的node接在node(X)上,而node(X)是node(Z)的
leftchild(亦即,新增的node之parent是parent->parent的leftchild); - 還有另外一半的情況就如圖五之右圖:將新增的node接在node(Y)上,而node(Y)是node(Z)的
rightchild(亦即,新增的node之parent是parent->parent的rightchild)。

圖五:。
必須要區分這兩者的原因有二:
- 一是
uncle:因為parent與uncle分別為parent->parent之leftchild與rightchild,若parent是left-,uncle就要是right-,反之亦然,兩者屬於互斥(exclusive)事件,不可能同時發生; - 二是Rotation(旋轉):在Case2與Case3中必須使用Left/Right Rotation,因此,延續第一點原因,考慮到
parent是leftchild或是rightchild的不同,Left/Right Rotation的方向也會相反。
程式碼
InsertFixedUpRBT()之範例程式碼分成以下幾個部分:
- 定義
color:\(0\)為紅色,\(1\)為黑色; - 如同圖四所示,修正的過程可能歷經不止一個Case,因此利用
while迴圈實現,條件式便是判斷當前current之parent是否為紅色; - 分別進行Case1(圖一(b)與圖一(c))、Case2(圖一(j))與Case3(圖一(f))之修正;
- 最後,有一行
root->color=1,確保root之顏色是黑色,這是為了Case1所設,由於Case1之修正方法是把「紅色與紅色node相連」之可能性往root方向傳遞,有可能root恰好是current的grandparent而被塗成紅色,如圖六,但因為RBT之第二點特徵要求root一定是黑色,因此必須作此預防。

圖六:。
// C++ code
void RBT::InsertFixedUpRBT(TreeNode *current){
// case0: parent是黑色, 就不用進回圈
while (current->parent->color == 0) { // 若parent是紅色即進入迴圈
// 上半部:parent是grandparent的left child
if (current->parent == current->parent->parent->leftchild) {
TreeNode *uncle = current->parent->parent->rightchild;
// case1: 若uncle是紅色
if (uncle->color == 0) {
current->parent->color = 1;
uncle->color = 1;
current->parent->parent->color = 0; //grandparent改成紅色
current = current->parent->parent;
}
// case2 & 3: uncle是黑色
else {
if (current == current->parent->rightchild){ // case2
current = current->parent;
LeftRotation(current);
}
// case3
current->parent->color = 1; //把parent塗黑
current->parent->parent->color = 0; // grandparent塗紅
RightRotation(current->parent->parent);
}
}
// 下半部:parent是grandparent的right child, 與上半部對稱
else {
TreeNode *uncle = current->parent->parent->leftchild;
// case1: 若uncle是紅色
if (uncle->color == 0) {
current->parent->color = 1;
uncle->color = 1;
current->parent->parent->color = 0; //grandparent改成紅色
current = current->parent->parent;
}
// case2 & 3: uncle是黑色
else {
if (current == current->parent->leftchild) { // case2
current = current->parent;
RightRotation(current);
}
// case3
current->parent->color = 1;
current->parent->parent->color = 0;
LeftRotation(current->parent->parent);
}
}
}
root->color = 1; // 確保root是黑色
}
以上便是於Red Black Tree(紅黑樹)中進行Insert(新增資料)與Insert後的Fixup(修正)之介紹。
下一篇文章將介紹於Red Black Tree(紅黑樹)中進行Delete(刪除資料)與Delete後的Fixup(修正)。
參考資料:
- Introduction to Algorithms, Ch13
- Fundamentals of Data Structures in C++, Ch10
- GeeksforGeeks:Red Black Tree
- Binary Search Tree: Search(搜尋資料)、Insert(新增資料)
RBT系列文章
Red Black Tree: Intro(簡介)
Red Black Tree: Rotation(旋轉)
Red Black Tree: Insert(新增資料)與Fixup(修正)
Red Black Tree: Delete(刪除資料)與Fixup(修正)
回到目錄: