Binary Tree: 建立一棵Binary Tree

Posted by Chiu CC on 12 27, 2015


先備知識與注意事項

在Binary Tree：Traversal中，非常沒誠意地用暴力方式建了一棵Binary Tree，在本篇文章將提供一種文明的方法，由一個字元陣列(char array)輸入字母，並按照Complete Binary Tree之順序重新建立那顆樹。

其中，問題情境之輸入資料是一個字元陣列(char array)，為了方便處理，將會使用C++語言中的神器：stringstream，這裡礙於篇幅(與筆者自己也還在摸索)，就不多談避免誤導，點進連結中有非常詳細的說明，關於istringstream、ostringstream、stringstream等等template class之繼承關係(inheritance)。

因為要按照Complete Binary Tree的規則建樹，可以想像的是，以下提供的Binary Tree之建立方法，基本上是在Binary Tree：Traversal介紹過的level-order traversal上加工，因此Queue(佇列)的概念會再次出現。

目錄


問題描述

問題描述如下：

  • 給定一個字元陣列，欲按照Complete Binary Tree之位置規則建立一棵Binary Tree，若陣列元素之資料為大寫字母(ASCII：\(65\)~\(90\))，則將其建立成Tree的node，若陣列元素為 ' x ' 則表示該位置沒有node。

以Binary Tree：Traversal中所提到的Binary Tree為例，如圖一：

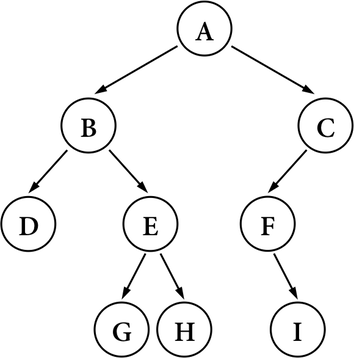
binary tree

圖一：。

其所對應的字元陣列即為：A B C D E F x x x G H x I，如圖二所示：

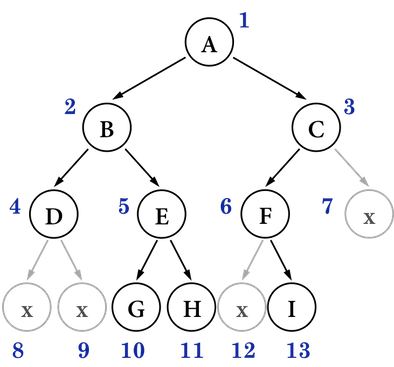
binary tree of char array

圖二：。

以下程式範例的目的就是要以如此文明的方式建立出如圖一的Binary Tree。


程式碼

(完整範例程式碼也可以看這裡：BT_Construct_from_char_array.cpp)

先看看main()中，上半部分別為：

  • 原始資料：字元陣列；
  • 以字元陣列建立一棵如圖二的Binary Tree，本篇重點在此；
  • 以inorder traversal印出樹的資料。

binary tree of char array

圖二：。

下半部則是示範以queue實現level-order traversal之小應用：以Complete Binary Tree之位置規則在樹中新增node，最後會把圖二之Binary Tree裡的「洞」給補起來，如圖四(b)。

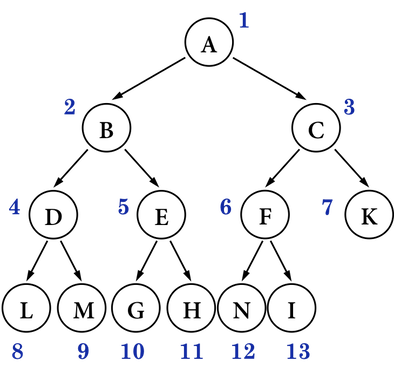
insertLMN

圖四(b)：。

溫馨小提醒：純粹以inorder traversal之結果並無法驗證樹之結構正如圖一(舉例來說：以inorder traversal對某個Linked list也可能得出相同結果)，因此，建議還是使用任何可取得的debugger把pointer全部攤開。

// C++ code
#include <iostream>
#include <sstream>
#include <queue>

int main() {
    const char *a = "A B C D E F x x x G H x I";
    BinaryTree T(a);                // 以level-order規則建立Binary Tree
    T.Inorder_by_parent();      // 以inorder-traversal印出Binary Tree
    std::cout << std::endl;

    T.InsertLevelorder('K');
    T.InsertLevelorder('L');
    T.InsertLevelorder('M');
    T.InsertLevelorder('N');
    T.Inorder_by_parent();
    std::cout << std::endl;

    return 0;
}

在經過一連串程式碼後，預期得到的output：

D B G E H A F I C   
L D M B G E H A N F I C K


定義class TreeNode、class BinaryTree

這裡對class TreeNode與class BinaryTree之定義，與上一篇文章之最大不同在於資料的隱蔽性，因為在此不需要在main()中存取任何pointer(root、leftchild、rightchild)，因此將之放進private區塊。

在class BinaryTree除了上一篇介紹過的inorder traversal外，多了兩個新朋友LevelorderConstruct()與InsertLevelorder()，前者即是本篇主角，吃進stringstream後，把樹建出來；後者純粹是好玩，其功能為「以Complete Binary Tree之位置規則，在理應出現node的位置，新增node」，能夠儘量減少在新增node時增加樹高(height)。

關於Inorder-traversal的三個函式leftmost()、InorderSuccessor()以及Inorder_by_parent()請參考上一篇：Binary Tree:Traversal(尋訪)/In-Order Traversal by Parent Field。

// C++ code
class BinaryTree;
class TreeNode{
private:
    TreeNode *leftchild;
    TreeNode *rightchild;
    TreeNode *parent;
    char data;
public:
    TreeNode():leftchild(0),rightchild(0),parent(0),data('x'){};
    TreeNode(char s):leftchild(0),rightchild(0),parent(0),data(s){};

    friend class BinaryTree;
};

class BinaryTree{
private:
    TreeNode *root;
public:
    BinaryTree():root(0){};
    BinaryTree(const char* str);

    void LevelorderConstruct(std::stringstream &ss);
    void InsertLevelorder(char data);

    TreeNode* leftmost(TreeNode *current);
    TreeNode* InorderSuccessor(TreeNode *current);
    void Inorder_by_parent();
};


Constructor of BinaryTree

class BinaryTree的constructor很直觀，拿到一個字元陣列，先送進stringstream後，再由stringstream放進樹中。

此處先對樹的root進行記憶體配置以及賦值，剩下的字母將利用LevelorderConstruct()以level-order的方式建立出Binary Tree。

// C++ code
BinaryTree::BinaryTree(const char* str){
    std::stringstream  ss;
    ss << str;                     // magic!

    root = new TreeNode;           // allocate memory for root
    ss >> root->data;              // assign character to root

    LevelorderConstruct(ss);
}


Function：LevelorderConstruct

在看LevelorderConstruct()的函式主體之前，再看一眼level-order traversal，概念上即是藉著queue的「先排隊就先購票」特性，在同一個level中，只要確保由左至右將node放進queue中，便能確保在進入下一個level後，以先前放入node之順序進行visiting。

整份程式碼的關鍵在於神器stringstream &ss，只要不斷地透過ss >> data，ss便會自動尋找下一筆資料(字母)餵進data。

while的條件式表示，若ss >> data失敗，也就是再也無法從ss拿到字母放進data，意味者所有字母已經全數檢查/輸入完畢，即結束迴圈。

在while內，新增條件用來判斷從stringstream中輸出的字母是「大寫字母」(ASCII：\(65\)~\(90\))還是「x」，前者要放入樹中建成node，後者則忽略不計。

在每一次迴圈中，會利用ss >> data輸入兩個字母，分別為current的leftchild與rightchild，因此，如果原本字元陣列是奇數筆資料，就會在while迴圈的中間輸入完畢，即跳出迴圈。

LevelorderConstruct()程式定義如下：

// C++ code
void BinaryTree::LevelorderConstruct(std::stringstream &ss){

    std::queue<TreeNode*> q;         // create a queue to handle level-roder rule
    TreeNode *current = root;        // point *current to root
    char data = 'x';                 // initializa data as 'x'

    while (ss >> data) {
        if (data >= 65 && data <= 90){                // 處理current的leftchild
            TreeNode *new_node = new TreeNode(data);  // call constructor TreeNode(char s)
            new_node->parent = current;
            current->leftchild = new_node;
            q.push(new_node);
        }
        if (!(ss >> data)){                           // 有可能char array含有奇數筆資料
            break;                                    // 所以在這裡結束迴圈
        }
        if (data >= 65 && data <= 90){                // 處理current的rightchild
            TreeNode *new_node = new TreeNode;        // call constructor TreeNode()
            new_node->parent = current;
            current->rightchild = new_node;
            new_node->data = data;                    // assign data to new_node
            q.push(new_node);
        }
        current = q.front();                          // 從queue中更新current
        q.pop();                                      // 更新queue
    }
}

詳細步驟如下：

  • 首先，在Binary Tree的constructor中，先配置root的記憶體位置，並透過第一次ss >> root->data將第一個字母放進root中，如圖三(a)。

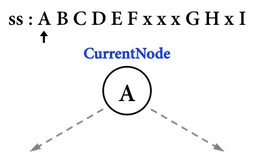
construct_0

圖三(a)：從ss取出第一個字母'A'放進root。

接著進入while迴圈。

  • 條件式：ss >> data若為真，表示成功從ss中取出字母，傳進data。
  • 進入迴圈後，先判斷取出的字母若為大寫字母(在此為'B')，即生成一個新的new_node。
  • 接著將B放進new_node中(這裡是透過class TreeNode的constructor完成)，並將CurrentNode(在此為A)的left child指向new_node，如圖三(b)。
  • 在queue 的部分，若成功建立出新的node(此為B)，便把B放進queue的隊伍中，表示之後將要把CurrentNode移到B，繼續往下建立新的node。

construct_1

圖三(b)：。

在同一個迴圈裡，建立完CurrentNode的left child後，接著嘗試建立right child。

  • 條件式：if( !(ss >> data) )若為真，表示ss中的字母已經讀取完畢，即跳出迴圈(break)。若否，則繼續從ss中讀取字母。
  • 判斷字母是否為大寫字母(此為'C')，便如同生成left child之方法，建立新的new_node、配置記憶體、將字母'C'放進new_node中，並將CurrentNode之right child指向new_node，如圖三(c)。
  • 已成功建立新的node(C)，便把C放進queue的隊伍中，表示之後將要把CurrentNode移到B，繼續往下建立新的node。

此時，queue裡有兩個node，分別為B與C，要注意的是，排隊時，先進入隊伍的人會代表隊伍的前方，因此B為queue的Front，C為queue的Back。

construct_2

圖三(c)：。

在建立完CurrentNode的left child與right child後，接著要移動CurrentNode，作為下一個while迴圈的起點。

queue的功能便是提供CurrentNode移動的依據：

  • 一律將queue隊伍的第一個node視作新的CurrentNode：
    • CurrentNode = q.front();。
  • 將CurrentNode移動至B後，便把B從queue移除(q.pop();)，如圖三(d)。

如此便能保證，CurrentNode的移動會依照level-order「由上至下、由左至右」之順序。

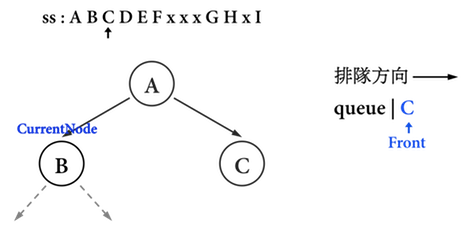
construct_3

圖三(d)：。

進入第二次while迴圈後，重複以上之步驟：

  • 從ss取出字母，放進data。
  • 判斷data是否為大寫，若是，便依序在CurrentNode之left child與right child建立新的node。
  • 並且，將成功建立之node放進queue隊伍中，用作之後CurrentNode移動之用。

仔細觀察圖三(e)至圖三(h)之ss與CurrentNode之移動，與queue的變化：

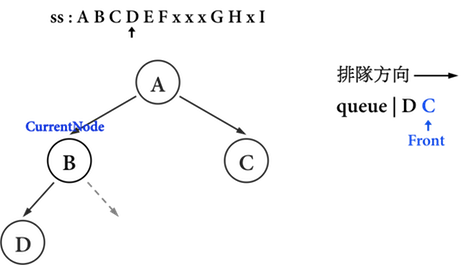
construct_4

圖三(e)：。

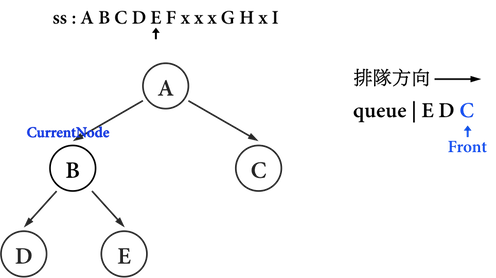
construct_5

圖三(f)：。

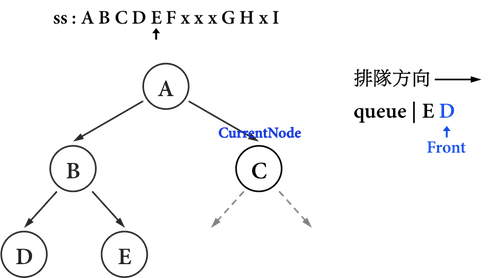
construct_6

圖三(g)：。

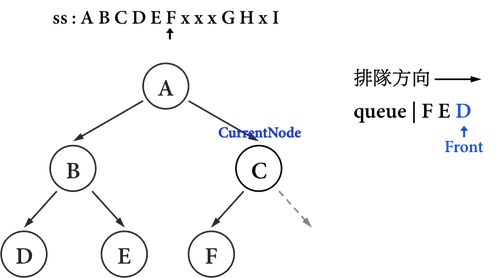
construct_7

圖三(h)：。

  • 在建立完C的left child後，從ss讀取到字母'x'，因為其並非大寫字母，表示C沒有right child，因此跳過生成新的node之步驟，如圖三(i)。

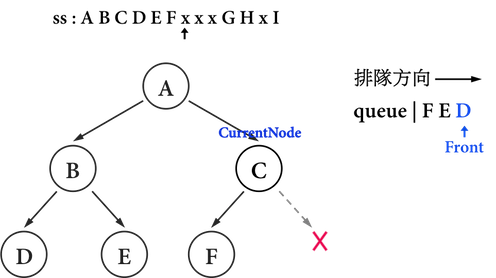
construct_8

圖三(i)：。

  • 若沒有生成新的node，便沒有新的node進入queue排隊。
  • 接著要繼續將CurrentNode移動到queue的第一個元素，也就是D，並把D從queue中移除，如圖三(j)。

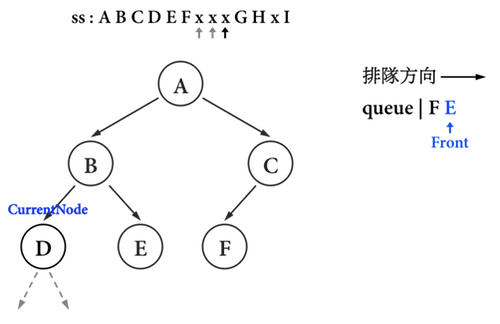
construct_9

圖三(j)：。

  • 當CurrentNode移動到D之後，ss連續放兩個'x'進入data，表示D的兩個child pointer皆指向NULL。
  • 由於沒有新的node產生，queue的隊伍便沒有更新，如圖三(k)。

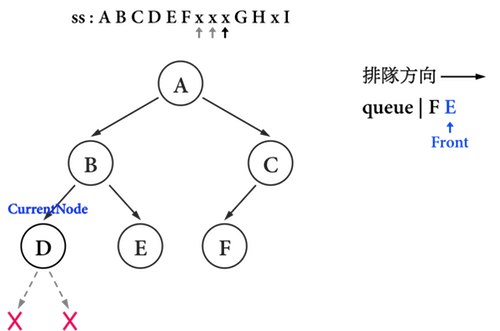
construct_10

圖三(k)：。

接著，重複步驟：

  • 移動CurrentNode至queue的第一個元素所指示的node。
  • 從ss讀取字母，判斷其若為大寫字母，便配置記憶體、產生新的node接在CurrentNode的child pointer上。
  • 若有生成新的node，則將該node推入queue的隊伍。

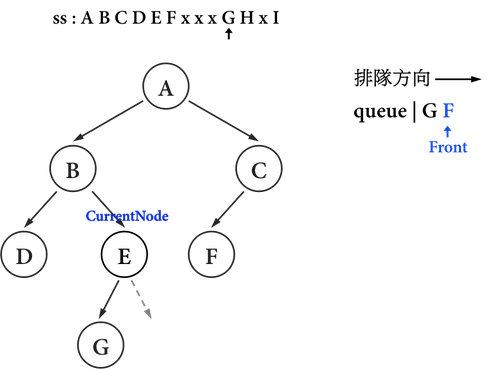
construct_11

圖三(l)：。

  • 直到ss輸出最後一個字母'I'後，這棵樹便建立完成。
  • 由於，ss已全數讀取完畢，敘述句：ss >> data不成立，因此結束迴圈。

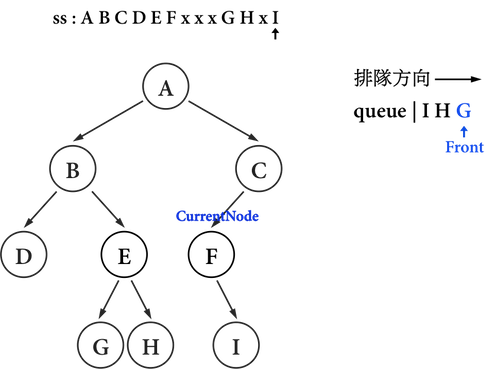
construct_12

圖三(m)：。



Function：InsertLevelorder

函式InsertLevelorder()的功能是，能夠按照Complete Binary Tree的位置順序放置新增的node，例如，若要在圖三之樹上新增帶有字母'K'的node，則T.InsertLevelorder('K')便會將'K'建成C的right child，如圖四(a)：

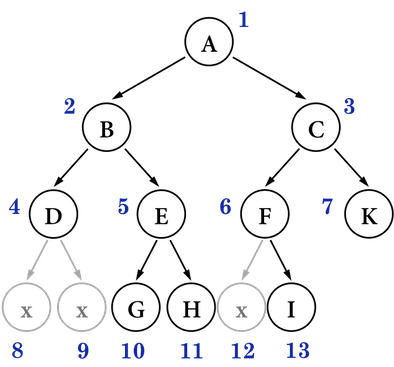
insertK

圖四(a)：。

再依序新增L、M、N：

  • T.InsertLevelorder('L');
  • T.InsertLevelorder('M');
  • T.InsertLevelorder('N');

即會得到如圖四(b)的樹：

insertLMN

圖四(b)：。

程式碼之邏輯與LevelorderConstruct()大同小異，最主要的部分就是利用queue來記錄CurrentNode移動的順序：

  • 首先，將current設成root，若樹存在，則進入while迴圈。
  • 接著要開始「找空位」，若current之left child已經有node，則將之放入queue中，在下次迴圈將以此node作為current，若left child還沒有node，便產生帶有data之新node，並將其建立成current之left child。
    當「parent指向child」與「child指向parent」的pointer連接完成後，便結束迴圈。
  • 對current之right child進行相同之步驟。

如此便能有效控制Binary Tree之樹高(height)，使pointer所配置之記憶體空間有效利用，亦能夠減少traversal(以及其他操作)所需的時間。

// C++ code
void BinaryTree::InsertLevelorder(char data){    

    std::queue<TreeNode*> q;
    TreeNode *current = root;

    while (current) {
        if (current->leftchild != NULL){               // current的leftchild沒有空位
            q.push(current->leftchild);                // 將其推進queue中
        }
        else{                                          // current的leftchild有空位
            TreeNode *new_node = new TreeNode(data);   // 建立新的node, 將字母放在這裡
            new_node->parent = current;
            current->leftchild = new_node;
            break;                         
        }
        if (current->rightchild != NULL) {             // current的rightchild沒有空位
            q.push(current->rightchild);               // 將其推進queue中
        }
        else{                                          // current的rightchild有空位
            TreeNode *new_node = new TreeNode(data);   // 建立新的node, 將字母放在這裡
            new_node->parent = current;                
            current->rightchild = new_node;
            break;
        }
        current = q.front();
        q.pop();
    }
}



以上便是利用queue執行level-order方式建立Binary Tree之範例。
另外，利用遞迴的方式，外帶一個迴圈來進行level-order traversal，也能夠完成相同的功能。


參考資料：


Binary Tree系列文章

Binary Tree: Intro(簡介)
Binary Tree: Traversal(尋訪)
Binary Tree: 建立一棵Binary Tree

回到目錄：

目錄：演算法與資料結構


tags: C++, Binary Tree, Queue,