先備知識與注意事項
Sorting(排序)是基本的資料處理,舉例來說,進入圖書館的查詢系統,不論是想按照「出版日期」或是「相關程度」找書,都會得到「排序過」的結果。
常見的Comparison Sort及其時間複雜度如表一,假設問題有\(N\)筆資料:
| Quick Sort | Merge Sort | Heap Sort | Insertion Sort | Selection Sort | |
|---|---|---|---|---|---|
| best case | \(N\log N\) | \(N\log N\) | \(N\log N\) | \(N\) | \(N^2\) |
| average case | \(N\log N\) | \(N\log N\) | \(N\log N\) | \(N^2\) | \(N^2\) |
| worst case | \(N^2\) | \(N\log N\) | \(N\log N\) | \(N^2\) | \(N^2\) |
表一:五種排序法之時間複雜度比較
Binary Heap可以分為Min Heap與Max Heap兩種。兩者用在排序上,僅僅是順序「由大到小」和「由小到大」的差別。
本篇文章將介紹以Max Heap實現Heap Sort(堆積排序法)的方法。
有關Min Heap的內容,請參考Priority Queue:Binary Heap。
目錄
Binary Heap(二元堆積)
Binary Heap有兩項基本特徵:
特徵一:Binary Heap之結構可以視作Complete Binary Tree。
- 如圖一(a),數值\(1\)~\(9\),一共有9個元素,按照Complete Binary Tree之順序規則,填滿位置\(1\)~\(9\),以index(\(1\))~index(\(9\))表示。
這樣的優點是方便尋找「parent-child」之關係,以index(\(i\))的node為例:
- 其left child必定位在index(\(2i\));
- 其right child必定位在index(\(2i+1\));
- 其parent必定位在index(\(\lfloor i/2 \rfloor\))。
以圖一(a)中位於index(\(3\))之node(\(8\))為例:
- 其left child為index(\(6\))之node(\(2\));
- 其right child為index(\(7\))之node(\(3\));
- 其parent為index(\(1\))之node(\(9\))。
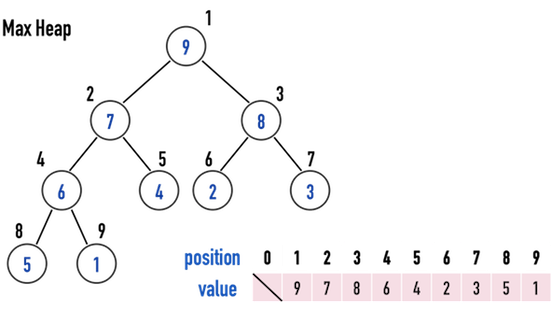
圖一(a):黑色數字是index,藍色數字是value。
特徵二:若將位於index(\(i\))之node視為subtree之root,那麼,可將此Binary Heap分為兩類:
-
Max Heap:在每一個subtree中,root之「數值」要比兩個child之「數值」還要大,見圖一(a):
- \(value(i)>value(2i)\)
- \(value(i)>value(2i+1)\)
-
Min Heap:在每一個subtree中,root之「數值」要比兩個child之「數值」還要小,見圖一(b):
- \(value(i)<value(2i)\)
- \(value(i)<value(2i+1)\)
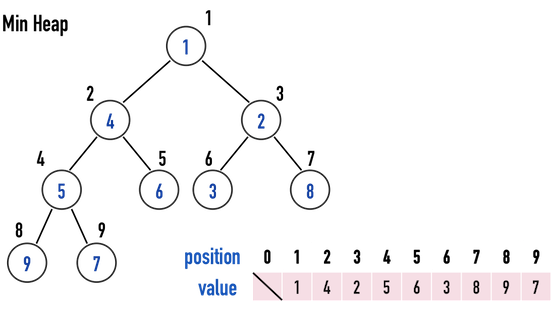
圖一(b)。
特別注意:在同一個subtree裡,leftchild(index(\(2i\)))與rightchild(index(\(2i+1\)))的「數值」大小順序不重要,只要和root(index(\(i\)))比較即可。
這也是Binary Heap與Binary Search Tree其中一項區別。
要滿足Binary Heap特有的「parent-child」之關係,只要讓矩陣中index(\(0\))的位置閒置,從index(\(1\))開始存放資料,即可使用矩陣(array)來表示Binary Heap。
接著介紹兩個函式,把任意矩陣轉換成Max Heap。
函式:MaxHeapify
MaxHeapify()的功能,是要「由上而下」地,以Max Heap的規則(root的數值「大於」兩個child的數值),調整矩陣。
以圖二(a)為例,觀察subtree「index(\(2\))-index(\(4\))-index(\(5\))」之「數值」:
- root:index(\(i=2\))為\(1\)
- leftchild:index(\(2i=4\))為\(9\)
- rightchild:index(\(2i+1=5\))為\(4\)
不符合Max Heap規則,所以要想辦法把這三個數值中的「最大值」,調整到index(\(i=2\)),也就是這棵subtree的root。
方法如下:
- 找到這三者的最大值,並以
int largest記錄該最大值的index。- 圖二(a)中,把
largest記錄為index(\(4\))。
- 圖二(a)中,把
- 將index(root)與index(largest)這兩個node互換位置,如此一來,當前的subtree必定能滿足Max Heap規則。
- 圖二(b)中,將index(\(2\))與index(\(4\))的node互換。
- subtree「index(\(2\))-index(\(4\))-index(\(5\))」的數值分別為「\(9-1-4\)」,符合Max Heap。
- 繼續以index(largest)當作新的subtree的root,檢查新的subtree是否符合Max Heap規則。
- 圖二(b)中,subtree「index(\(4\))-index(\(8\))-index(\(9\))」再次不滿足Max Heap,便重複上述步驟,得到圖二(c)。
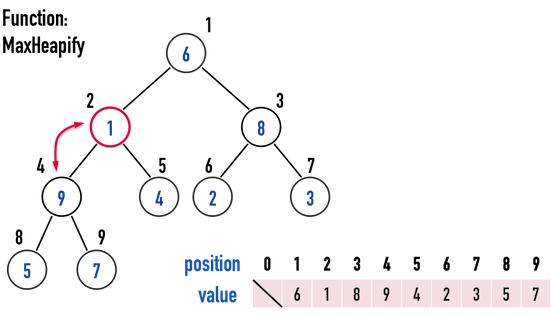
圖二(a)。
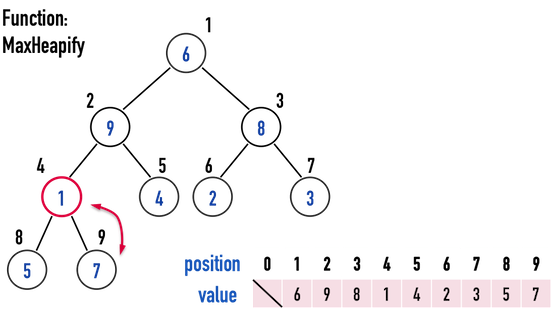
圖二(b)。
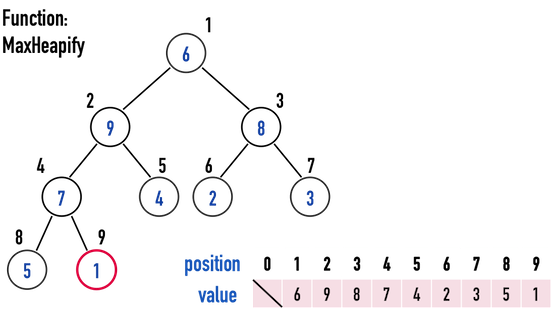
圖二(c)。
如此一來,有被MaxHeapify()檢查過的subtree,都會符合Max Heap規則。
因此,只要對所有「具有child的node」檢查一次MaxHeapify(),便能夠把一個任意矩陣調整成Max Heap,這就是下一個函式BuildMaxHeap()的功能。
函式:BuildMaxHeap
有了MaxHeapify()之後,只要對所有「具有child的node」進行MaxHeapify(),也就是位於index(\(1\))\(~\)index(\(\lfloor N/2 \rfloor\))的node,就能夠將任意矩陣調整成Max Heap。
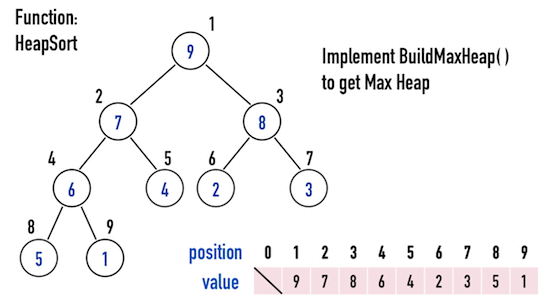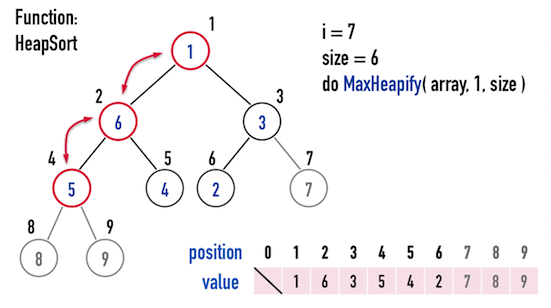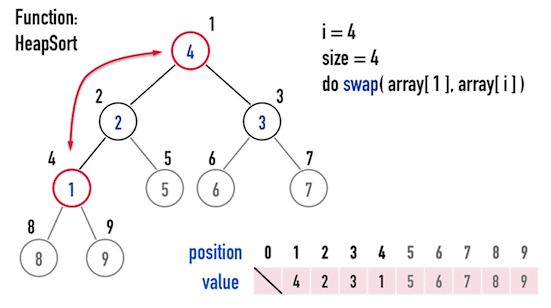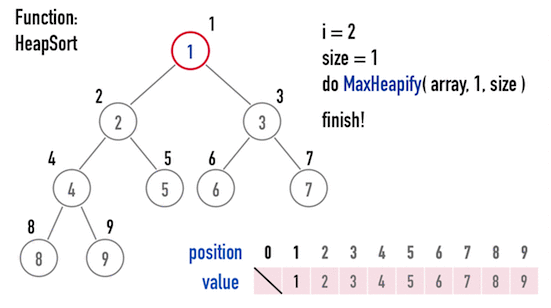
- 以圖三為例,Binary Heap共有\(9\)個node,便從index(\(4\))往index(\(1\)),逐一對node進行
MaxHeapify(),即可得到Max Heap。
為什麼只要對「具有child的node」調整呢?
因為Max Heap的規則是「比較root的數值與child的數值」,如果是沒有child的node(屬於leaf node),就一定不會違反Max Heap的規則。
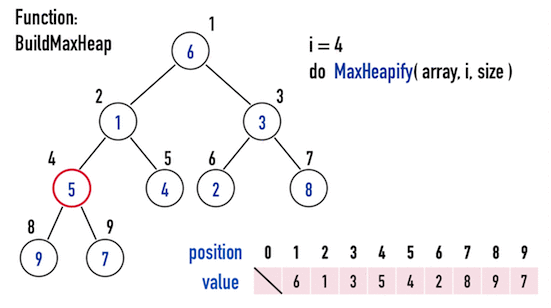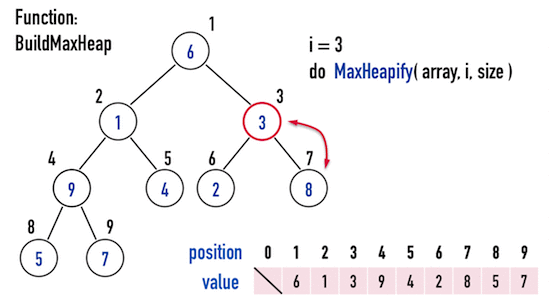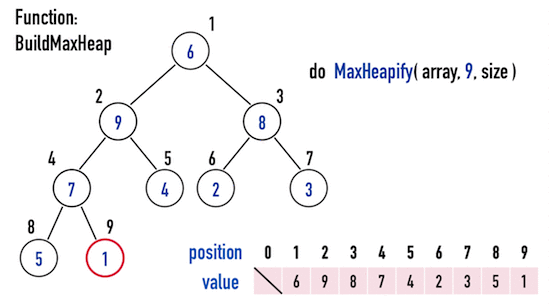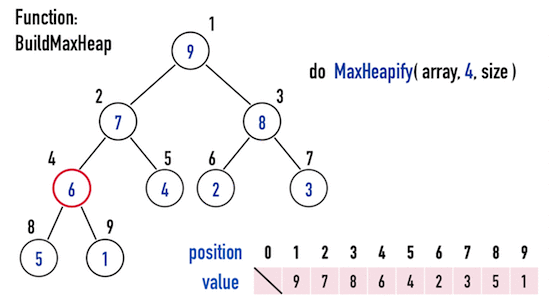
圖三。
Heap Sort(堆積排序法)
經過BuildMaxHeap()之後,便能將任意矩陣調整成Max Heap。
那麼要如何將此Max Heap做排序呢?
Max Heap的特徵是「第一個node具有最大值」,如果要將資料「由小到大」排序,步驟如下:
- 把「第一個node」和「最後一個node」互換位置。
- 假裝heap的「最後一個node」從此消失不見。
- 對「第一個node」進行
MaxHeapify()。
重複以上步驟,從heap的最後一個node開始,一路往上,直到root,便能得到排好序的矩陣。
以圖四(a)的Max Heap為例,現要將其調整成「由小到大」排好序的矩陣。
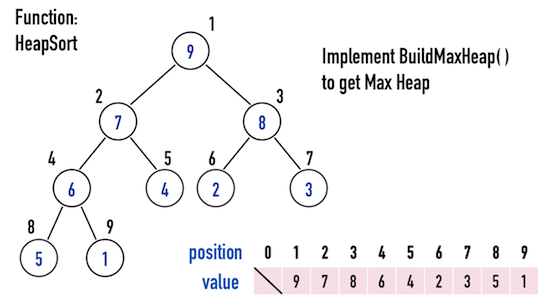
圖四(a)。
首先,從「最後一個位置」開始,將index(\(9\))的node與index(\(1\))的node互換位置,見圖四(b)。
如此,便把「最大值」的node(\(9\))給放到最後一個位置,以及「不是最大值」的node(\(1\))換到第一個位置。
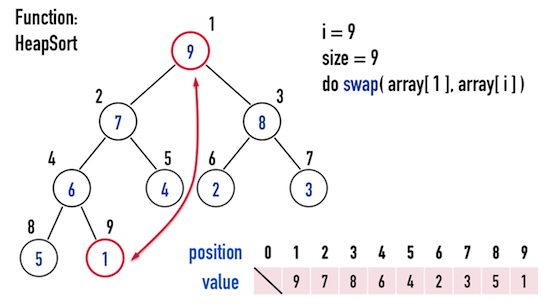
圖四(b)。
接著,最重要的概念就是「假裝最後一個node消失不見」:
- 因為此時,heap的「最後一個node」一定是「最大值」的node,也就表示,如果要得到「由小到大」的排序,那麼,此時便已經完成「最大值node」的調整。
同時,目前的index(\(1\))的node一定不是「最大值」,所以要利用MaxHeapify()重新調整「矩陣」,使其符合Max Heap規則。
又因為「假裝最後一個node消失不見」,所以,接下來要調整的「矩陣」,是「忽略index(\(9\))」的矩陣,因此只要考慮由「index(\(1\))~index(\(8\))」所形成的矩陣即可。
- 圖四(c)中的
size,即表示MaxHeapify()要處理的矩陣之size。 - 此次的
MaxHeapify()將會碰到subtree(index(\(1\))-index(\(2\))-index(\(3\)))與subtree(index(\(3\))-index(\(6\))-index(\(7\)))。
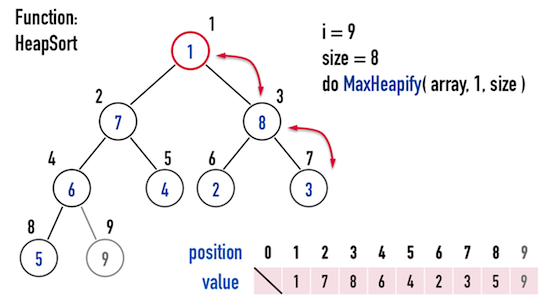
圖四(c)。
經過圖四(c)的MaxHeapify()調整,由「index(\(1\))~index(\(8\))」形成的矩陣,又再次滿足Max Heap,見圖四(d)。
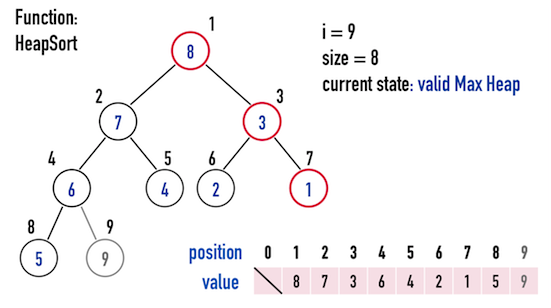
圖四(d)。
接著,再繼續重複上述步驟:
- 交換「目前考慮的矩陣」的「最後一個位置node」與「第一個node」;
- 以
MaxHeapify()調整「目前考慮的矩陣」。
便能得到「由小到大」排好序的矩陣,見圖四(e)。
圖四(e)。
程式碼
範例程式碼包含幾個部分:
swap():執行「交換node」。因為要實質交換array中的資料,所以必須使用reference或使pointer作為函式的參數(argument)。
MaxHeapify():「由上而下」,逐一檢查subtree,使subtree滿足Max Heap規則。函式的參數分別為
array:記錄heap的矩陣。root:當前的subtree之root的index。length:這是「目前要處理的矩陣」的長度,同時也用來判斷child是否超過矩陣長度。
BuildMaxHeap():對所有「具有child的node」進行MaxHeapify()。
HeapSort():將Max Heap轉換成「由小到大」排好序的矩陣。小細節:
- 因為heap是從index(\(1\))開始儲存資料,所以要先把index(\(0\))給空下來,最後再將其刪除。
- 這裡是利用
std::vector<int>的成員函式(member function)「insert()」與「erase()」處理。 關於std::vector,請參考:Cplusplus:std::vector。
以及main(),建立矩陣,並執行HeapSort(),驗證結果。
// C++ code
#include <iostream>
#include <vector>
void swap(int &p1, int &p2){
int temp = p1;
p1 = p2;
p2 = temp;
}
void MaxHeapify(std::vector<int> &array, int root, int length){
int left = 2*root, // 取得left child
right = 2*root + 1, // 取得right child
largest; // largest用來記錄包含root與child, 三者之中Key最大的node
if (left <= length && array[left] > array[root])
largest = left;
else
largest = root;
if (right <= length && array[right] > array[largest])
largest = right;
if (largest != root) { // 如果目前root的Key不是三者中的最大
swap(array[largest], array[root]); // 就調換root與三者中Key最大的node之位置
MaxHeapify(array, largest, length); // 調整新的subtree成Max Heap
}
}
void BuildMaxHeap(std::vector<int> &array){
for (int i = (int)array.size()/2; i >= 1 ; i--) {
MaxHeapify(array, i, (int)array.size() - 1); // length要減一, 因為heap從1開始存放資料
}
}
void HeapSort(std::vector<int> &array){
array.insert(array.begin(), 0); // 將index(0)閒置
BuildMaxHeap(array); // 將array調整成Max Heap
int size = (int)array.size() -1; // size用來記錄「目前要處理的矩陣」之長度
for (int i = (int)array.size() -1; i >= 2; i--) {
swap(array[1], array[i]); // 將最大值放到array的最後一個位置
size--;
MaxHeapify(array, 1, size); // 調整「忽略最後一個位置」的矩陣
}
array.erase(array.begin()); // 將index(0)刪除
}
void PrintArray(std::vector<int> &array){
for (int i = 0; i < array.size(); i++) {
std::cout << array[i] << " ";
}
std::cout << std::endl;
}
int main() {
int arr = {9, 4, 1, 6, 7, 3, 8, 2, 5};
std::vector<int> array(arr, arr+sizeof(arr)/sizeof(int));
std::cout << "original:\n";
PrintArray(array);
HeapSort(array);
std::cout << "sorted:\n";
PrintArray(array);
return 0;
}
output:
original:
9 4 1 6 7 3 8 2 5
sorted:
1 2 3 4 5 6 7 8 9
以上便是以Max Heap實現Heap Sort之介紹。
參考資料:
- Introduction to Algorithms, Ch6
- Fundamentals of Data Structures in C++, Ch5, Ch7
- Priority Queue:Intro(簡介) & Binary Heap
- Cplusplus:std::vector
Comparison Sort系列文章
Comparison Sort: Insertion Sort(插入排序法)
Comparison Sort: Quick Sort(快速排序法)
Comparison Sort: Heap Sort(堆積排序法)
Comparison Sort: Merge Sort(合併排序法)
回到目錄: