先備知識與注意事項
Sorting(排序)是基本的資料處理,舉例來說,進入圖書館的查詢系統,不論是想按照「出版日期」或是「相關程度」找書,都會得到「排序過」的結果。
常見的Comparison Sort及其時間複雜度如表一,假設問題有\(N\)筆資料:
| Quick Sort | Merge Sort | Heap Sort | Insertion Sort | Selection Sort | |
|---|---|---|---|---|---|
| best case | \(N\log N\) | \(N\log N\) | \(N\log N\) | \(N\) | \(N^2\) |
| average case | \(N\log N\) | \(N\log N\) | \(N\log N\) | \(N^2\) | \(N^2\) |
| worst case | \(N^2\) | \(N\log N\) | \(N\log N\) | \(N^2\) | \(N^2\) |
表一:五種排序法之時間複雜度比較
本篇文章將介紹Merge Sort(合併排序法)。
目錄
Merge Sort(合併排序法)
Merge Sort屬於Divide and Conquer演算法,把問題先拆解(divide)成子問題,並在逐一處理子問題後,將子問題的結果合併(conquer),如此便解決了原先的問題。
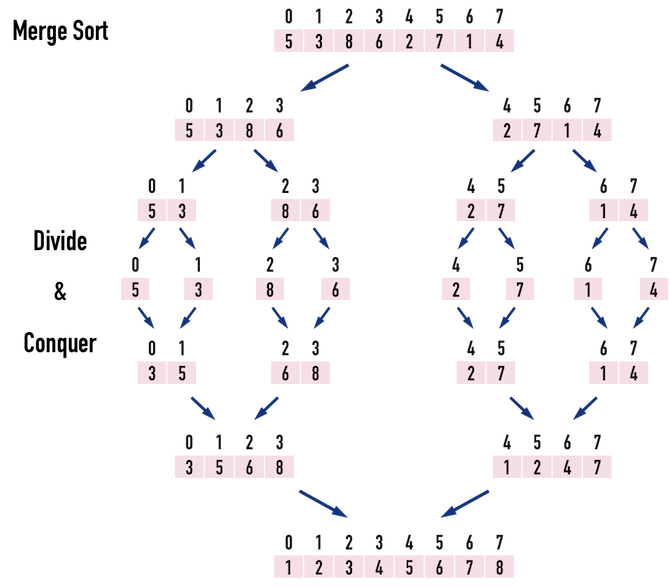
圖一。
以圖一為例,要把數列{\(5,3,8,6,2,7,1,4\)}排序成{\(1,2,3,4,5,6,7,8\)},Merge Sort的方法為:
- Divide:把數列「對半拆解」成兩個小數列。
- 先把{\(5,3,8,6,2,7,1,4\)}分成{\(5,3,8,6\)}與{\(2,7,1,4\)}。
- 再把{\(5,3,8,6\)}分解成{\(5,3\)}與{\(8,6\)}。
- {\(2,7,1,4\)}分解成{\(2,7\)}與{\(1,4\)}。
- 依此類推,直到每個數列剩下一個元素。
- Conquer:按照「由小到大」的順序,「合併」小數列。
- 考慮數列{\(5\)}與{\(3\)},比較大小後,合併成數列{\(3,5\)}。
- 考慮數列{\(8\)}與{\(6\)},比較大小後,合併成數列{\(6,8\)}。
- 考慮數列{\(3,5\)}與{\(6,8\)},比較大小後,合併成數列{\(3,5,6,8\)}。
- 依此類推,最後,考慮數列{\(3,5,6,8\)}與{\(1,2,4,7\)},比較大小後,合併成數列{\(1,2,3,4,5,6,7,8\)}。
即完成Merge Sort。
由圖一可以看出,在排序過程,需要先把{\(5\)}與{\(3\)}「記下來」,才能用來比較、合併出{\(3,5\)},需要先把{\(3,5\)}與{\(6,8\)}「記下來」,才能用來比較、合併出{\(3,5,6,8\)},因此,最直覺的方式,便是利用遞迴(recursion)來「記錄先前的狀態」:
void MergeSort(std::vector<int> &array, int front, int end){
// front與end為矩陣範圍
if (front < end) { // 表示目前的矩陣範圍是有效的
int mid = (front+end)/2; // mid即是將矩陣對半分的index
MergeSort(array, front, mid); // 繼續divide矩陣的前半段subarray
MergeSort(array, mid+1, end); // 繼續divide矩陣的後半段subarray
Merge(array, front, mid, end); // 將兩個subarray做比較, 並合併出排序後的矩陣
}
}
所以,關鍵就是Merge()的方法。
函式:Merge
以圖一中,合併數列{\(2,7\)}與{\(1,4\)}為例,見圖二(a)。
Merge()的大前提:若要由小數列合併出大數列,那麼各自的小數列必須「已經排好序」。
- 例如數列{\(2,7\)},已經「由小到大」排好序(\(2\)在\(7\)前面),數列{\(1,4\)}也已經排好序。
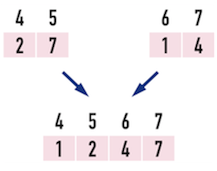
圖二(a)。
Merge()的詳細步驟如下,見圖二(b):
- 建立兩個新的矩陣(稱為
LeftSub[]與RightSub[]),分別記錄數列{\(2,7\)}與{\(1,4\)}。 - 並在兩個新矩陣的最後一個位置,新增一個值為「無限大」的元素。
- 這個「無限大」的元素是為了「比較」用。
接著便開始「比較兩個矩陣的元素」,挑選「較小的元素」放進原矩陣Array中。
- 目前要更新的是介於
Array[4]~Array[7]的矩陣元素。 - 以
int front代表\(4\),以int end代表\(7\),表示此範圍的頭尾。
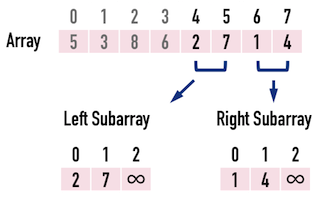
圖二(b)。
首先,替LeftSub[]與RightSub[]設立個別的index,稱為int idxLeft=0與int idxRight=0,見圖二(c)的紅色箭頭。

圖二(c)。
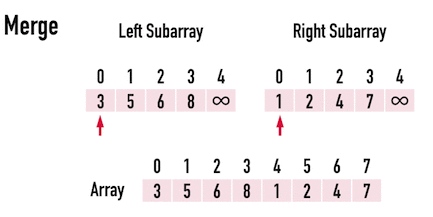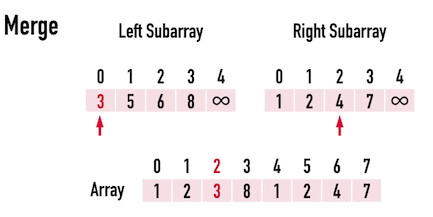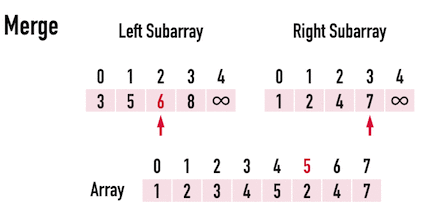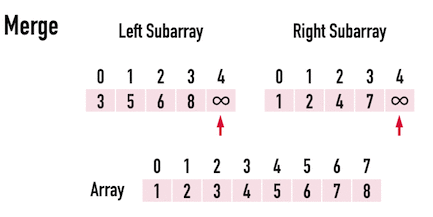
接著比較LeftSub[idxLeft=0]與RightSub[idxRight=0],發現後者較小,便將Array[front=4]更新成RightSub[idxRight=0]的\(1\),見圖二(d)。
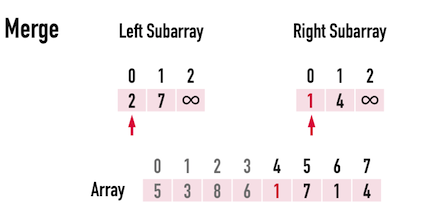
圖二(d)。
由於目前的RightSub[idxRight=0]已經放進Array裡,表示該元素\(1\)已經被調整完畢,於是便把idxRight往後移,繼續調整RightSub[]的其餘元素,見圖二(e)左。
以上便完成一次「比較兩個小矩陣之元素大小」並「更新原矩陣元素」之過程。
重複上述步驟,繼續更新Array[front+1]的矩陣元素值,直到Array[end=7],即可完成Array[4]~Array[7]的排序,見圖二(e)至圖二(g)。
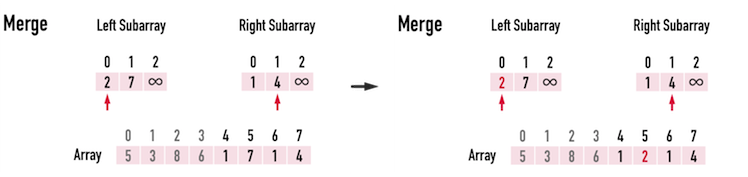
圖二(e)。
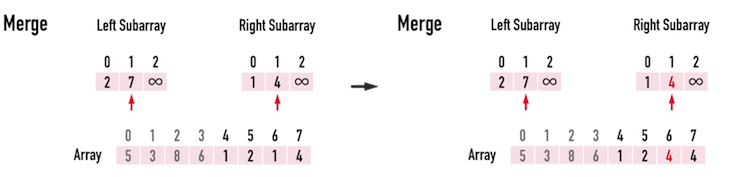
圖二(f)。
此時,idxRight移動到\(2\),而RightSub[2]為「無限大」,如此一來便表示,RightSub[]裡的元素都已經成功地排序進Array[]裡。
接下來在比較LeftSub[]與RightSub[]時,一定會選擇LeftSub[]的元素放進Array[]。
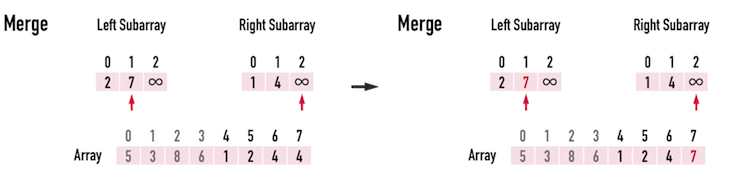
圖二(g)。
到目前為止,已經將Array[4]~Array[7]排序完成。
只要再將其與「排好序的」Array[0]~Array[3]進行「比較、合併」,即可完成Merge Sort,見圖二(h)。
圖二(h)。
程式碼
範例程式碼包含幾個部分:
MergeSort():以遞迴形式對數列進行Divide and Conquer。
Merge():合併數列的主要函式,其中使用了std::vector的成員函式(member function):constructor與insert(),來創造如圖二(b)的LeftSub[]與RightSub[]。
- 關於
std::vector,請參考:Cplusplus:std::vector。
以及main(),建立矩陣,並執行MergeSort(),驗證結果。
// C++ code
#include <iostream>
#include <vector>
const int Max = 1000;
void Merge(std::vector<int> &Array, int front, int mid, int end){
// 利用 std::vector 的constructor,
// 把array[front]~array[mid]放進 LeftSub[]
// 把array[mid+1]~array[end]放進 RightSub[]
std::vector<int> LeftSub(Array.begin()+front, Array.begin()+mid+1),
RightSub(Array.begin()+mid+1, Array.begin()+end+1);
LeftSub.insert(LeftSub.end(), Max); // 在LeftSub[]尾端加入值為 Max 的元素
RightSub.insert(RightSub.end(), Max); // 在RightSub[]尾端加入值為 Max 的元素
int idxLeft = 0, idxRight = 0;
for (int i = front; i <= end; i++) {
if (LeftSub[idxLeft] <= RightSub[idxRight] ) {
Array[i] = LeftSub[idxLeft];
idxLeft++;
}
else{
Array[i] = RightSub[idxRight];
idxRight++;
}
}
}
void MergeSort(std::vector<int> &array, int front, int end){
// front與end為矩陣範圍
if (front < end) { // 表示目前的矩陣範圍是有效的
int mid = (front+end)/2; // mid即是將矩陣對半分的index
MergeSort(array, front, mid); // 繼續divide矩陣的前半段subarray
MergeSort(array, mid+1, end); // 繼續divide矩陣的後半段subarray
Merge(array, front, mid, end); // 將兩個subarray做比較, 並合併出排序後的矩陣
}
}
void PrintArray(std::vector<int> &array){
for (int i = 0; i < array.size(); i++) {
std::cout << array[i] << " ";
}
std::cout << std::endl;
}
int main() {
int arr[] = {5,3,8,6,2,7,1,4};
std::vector<int> array(arr, arr+sizeof(arr)/sizeof(int));
std::cout << "original:\n";
PrintArray(array);
MergeSort(array, 0, 7);
std::cout << "sorted:\n";
PrintArray(array);
return 0;
}
output:
original:
5 3 8 6 2 7 1 4
sorted:
1 2 3 4 5 6 7 8
以上便是Merge Sort之介紹。
參考資料:
- Introduction to Algorithms, Ch2
- Fundamentals of Data Structures in C++, Ch7
- 小殘的程式光廊:合併排序法(Merge Sort)
- Infinite Loop:【演算】合併排序法 - Mergesort
- Cplusplus:std::vector
Comparison Sort系列文章
Comparison Sort: Insertion Sort(插入排序法)
Comparison Sort: Quick Sort(快速排序法)
Comparison Sort: Heap Sort(堆積排序法)
Comparison Sort: Merge Sort(合併排序法)
回到目錄: