Comparison Sort: Insertion Sort(插入排序法)

先備知識與注意事項

Sorting(排序)是基本的資料處理，舉例來說，進入圖書館的查詢系統，不論是想按照「出版日期」或是「相關程度」找書，都會得到「排序過」的結果。

常見的Comparison Sort及其時間複雜度如表一，假設問題有\(N\)筆資料：

	Quick Sort	Merge Sort	Heap Sort	Insertion Sort	Selection Sort
best case	\(N\log N\)	\(N\log N\)	\(N\log N\)	\(N\)	\(N^2\)
average case	\(N\log N\)	\(N\log N\)	\(N\log N\)	\(N^2\)	\(N^2\)
worst case	\(N^2\)	\(N\log N\)	\(N\log N\)	\(N^2\)	\(N^2\)

表一：五種排序法之時間複雜度比較

本篇文章將介紹Insertion Sort(插入排序法)。

Insertion Sort(插入排序法)

想像手上有一副撲克牌，若想要將紙牌從左到右按照「小到大」排序。

Insertion Sort的方法為：將第\(i\)張紙牌加入「前\(i-1\)張排序過」的紙牌組合，得到\(i\)張排序過的紙牌組合。

以圖一為例，從左邊數來的前三張紙牌已經排好序：index(0)、index(1)、index(2)分別為\(1、3、5\)，現在要將第四張紙牌(index(3)，數值為\(2\))加入前三張牌，想要得到「前四張排好序」的紙牌組合。
經由觀察，最終結果的紙牌順序為\(1、2、3、5\)，可以透過以下步驟完成：

原先index(2)的\(5\)搬到index(3)；
原先index(1)的\(3\)搬到index(2)；
原先index(3)的\(2\)搬到index(1)；

如此便能把第\(4\)張紙牌加入(insert)「前\(3\)張排序過」的紙牌組合，得到「前\(4\)張排序過」的紙牌組合。

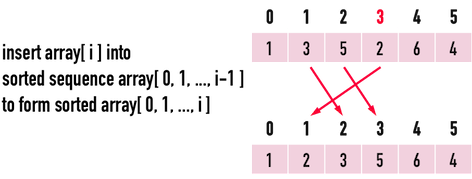
圖一：想像這是撲克牌。

由以上說明可以看出，Insertion Sort要求，在處理第\(i\)筆資料時，第\(1\)筆至第\(i-1\)筆資料必須先排好序。
那麼，只要按照順序，從第\(1\)筆資料開始處理，便能確保「處理第\(2\)筆資料時，第\(1\)筆資料已經排好序」，「處理第\(3\)筆資料時，第\(1\)筆、第\(2\)筆資料已經排好序」，依此類推，若共有\(N\)筆資料，必定能夠在處理第\(N\)筆資料時，將第\(1\)筆至第\(N-1\)筆資料排序過。

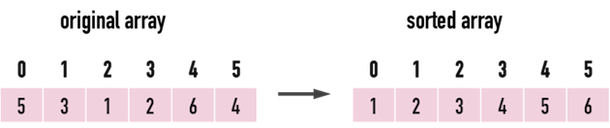
圖二。

以下將以圖二的矩陣資料為例，進行Insertion Sort，見圖三。

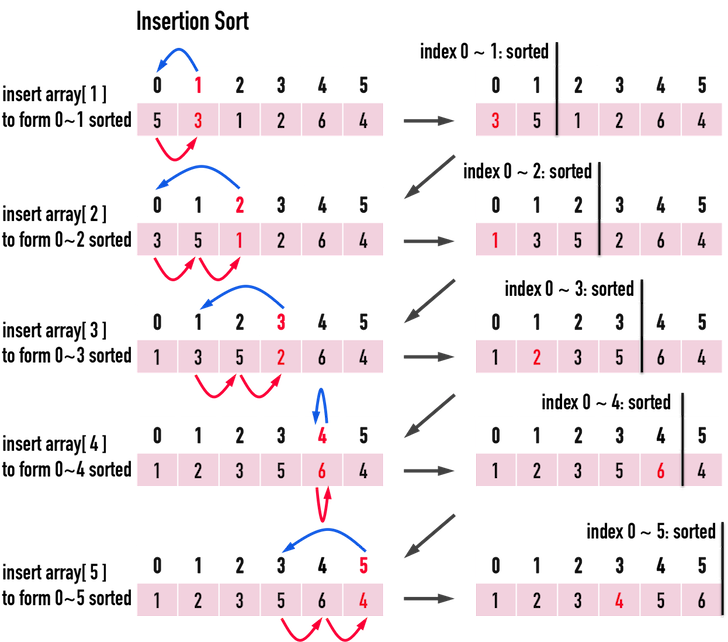
圖三。

那麼，第\(i\)筆資料要怎麼知道其在前\(1\)~\(i-1\)筆資料之間的順序位置？以圖三為例，當要將array[3]的\(2\)，加入array[0]~array[2]的數列時，要怎麼得知，其將被換到array[1]的位置？
就是要透過comparison(比較)。

詳細步驟如下：

現考慮將array[1]的\(3\)加入array[1]之前的數列，也就是與array[0]的\(5\)，一起形成「排好序」的array[0]~array[1]，見圖四(a)：

定義變數int i為「目前欲處理」的資料的index。
- 在此i=1，array[i]=3。
定義變數int j來表示「已經排好序」的數列的「最後一個」元素之index。
- 在此j=0，array[j]=5。
- int j會不斷遞減，j--，來檢查array[j]是否比「目前欲處理」的資料還大。
定義變數int key=array[i]，把「目前欲處理」的array[i]以key儲存，避免array[i]被覆蓋掉。

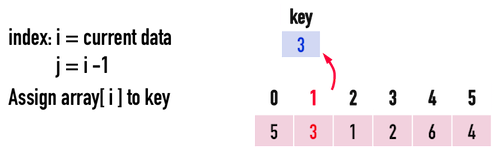
圖四(a)。

接著，比較key與array[j]的大小，同時確認index(j)沒有超出矩陣範圍。

若key<array[j](並且j>-1)，就表示「目前欲處理」的資料(原先位在index(i)的資料)，比array[j](也就是index(i-1)的資料)還要小，於是將array[j]「往後移」，見圖四(b)：

換位置的方式類似swap()，先執行array[j+1]=array[j]，也就是將原先的array[j]「往後移一個位置」。
- 在此，把\(5\)放進array[1]。
- 可以預期，原先\(5\)在的位置array[0]會被key給補上。如此便完成array[0]~array[1]的排序。
接著，因為不確定前\(1\)~\(i-1\)筆資料中，是否還有資料比key大，所以執行j--，繼續「往前」比較。
- 在此例，因為j--後，j等於\(-1\)，已經超過矩陣範圍，所以便結束程序。

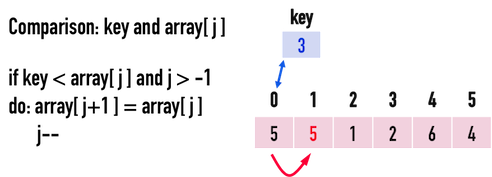
圖四(b)。

當兩項條件：j>-1與key<array[j]中，有任何一項條件不滿足時，便表示「已經檢查到前\(1\)~\(i-1\)筆資料的盡頭」，或是「已經沒有比key還小的資料」，於是便執行array[j+1]=key，把key放回矩陣裡，見圖四(c)。

當不滿足上述兩項條件時，j+1就會是key的位置。
在此，j等於\(-1\)，j+1等於\(0\)，表示key是\(1\)~\(i\)筆資料中，最小的資料。

以上步驟，便完成array[0]~array[1]的排序。

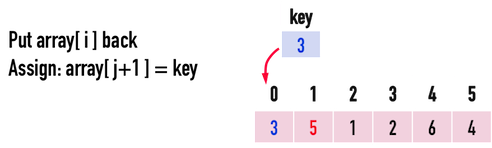
圖四(c)。

目前為止，可以確定array[0]~array[1]已經排好序，便能夠再接著將array[2]加入前面兩項，完成array[0]~array[2]的排序，見圖四(d)。

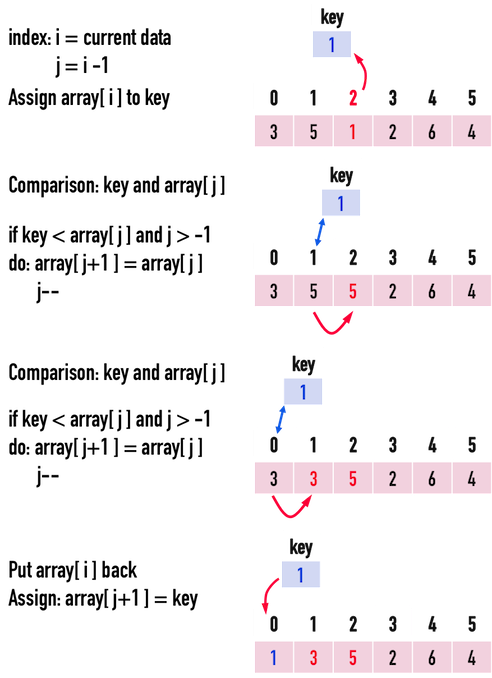
圖四(d)。

再看一次，要把array[3]放入array[0]~array[2]的排序中，形成array[0]~array[3]的排序。

其中，在比較key是否比array[0]還小時，發現key>array[j](key為\(2\)，array[j]為\(1\))，便不需要把array[0]「往後移」，並把key放進array[j+1]，完成array[0]~array[3]的排序。

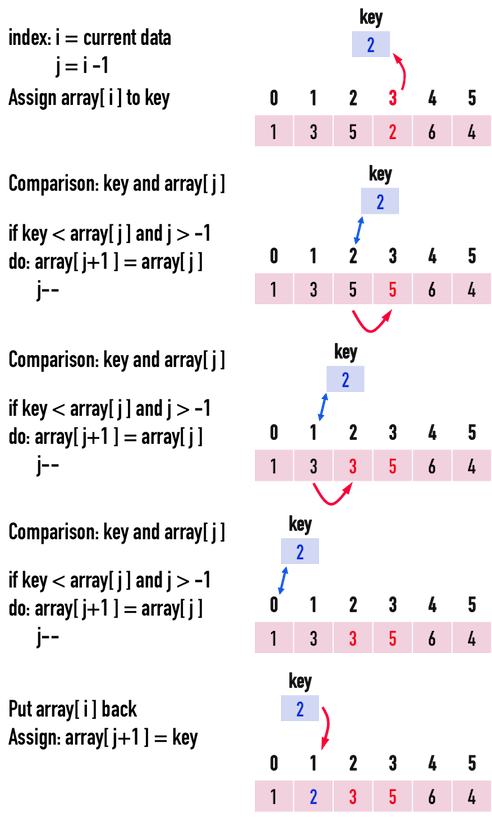
圖四(e)。

重複上述步驟，便可完成array[0]~array[5]的排序，如圖三所示。

程式碼

程式碼很直觀：

int i是「目前要處理」的資料index(i)；
int j=i-1是用來指出前\(1\)~\(i-1\)筆資料的index；
第一個for迴圈，用意是把每一個矩陣元素都視為「目前要處理」的資料一次；
在for迴圈裡的while迴圈，用意是把「目前要處理」的資料與前\(1\)~\(i-1\)筆資料做比較，並找到適當的位置，將\(1\)~\(i\)筆資料做排序。

以及main()，建立如圖二的矩陣，進行InsertionSort()，並將矩陣元素以PrintArray()印出。

// C++ code

#include <iostream>
void InsertionSort(int *arr, int size){

    for (int i = 1; i < size; i++) {
        int key = arr[i];
        int j = i - 1;
        while (key < arr[j] && j >= 0) {
            arr[j+1] = arr[j];
            j--;
        }
        arr[j+1] = key;
    }
}
void PrintArray(int *arr, int size){
    for (int i = 0; i < size; i++) {
        std::cout << arr[i] << " ";
    }
    std::cout << std::endl;
}
int main() {

    int array[6] = { 5, 3, 1, 2, 6, 4 };
    std::cout << "original:\n";
    PrintArray(array, 6);

    InsertionSort(array, 6);

    std::cout << "sorted:\n";
    PrintArray(array, 6);
    return 0;
}

output:

original:
5 4 1 2 6 4 
sorted:
1 2 4 4 5 6

以上便是Insertion Sort的介紹。

關於時間複雜度的部分：
(欲將資料由左至右以「小到大」排序)

best case：若要處理的序列是\(1、2、...、N\)，那麼只要比較\(N\)次即可完成排序，時間複雜度為\(O(N)\)，此即為。
- 依此推論，當問題已經「接近完成排序」的狀態時，使用Insertion Sort會非常有效率。
worst case：若要處理的序列恰好是顛倒順序，\(N、N-1、...、2、1\)，那麼位於index(i)的元素，需要比較「\(i-1\)次」，完成演算法總共要比較\(frac{N(N-1)}{2}\)次，時間複雜度為\(O(N^2)\)。
average case：時間複雜度也是\(O(N^2)\)。
- 詳情請參考：Mordecai Golin：Average Case Analysis of Insertionsort。

當問題的資料量較小時(欲排序的元素之數目較小)，使用Insertion Sort會很有效率，這是因為和Quick Sort、Merge Sort、Heap Sort相比，Insertion Sort不具有「遞迴」形式，因此不需要系統的stack，詳情請參考：

再加上前面提到的best case特徵，有些演算法會在Quick Sort中加入Insertion Sort，讓剩下的「接近完成排序」的資料以Insertion Sort處理，使排序更有效率，詳情請參考：

Stackoverflow：How to optimize quicksort

參考資料：

Comparison Sort系列文章

Comparison Sort: Insertion Sort(插入排序法)
Comparison Sort: Quick Sort(快速排序法)
Comparison Sort: Heap Sort(堆積排序法)
Comparison Sort: Merge Sort(合併排序法)

回到目錄：

目錄：演算法與資料結構