Complexity：Asymptotic Notation(漸進符號)

先備知識與注意事項

本篇文章將介紹Complexity(複雜度)，以及用來分析Complexity(複雜度)的Asymptotic Notation(漸進符號)。

Complexity(複雜度)

圖一：。

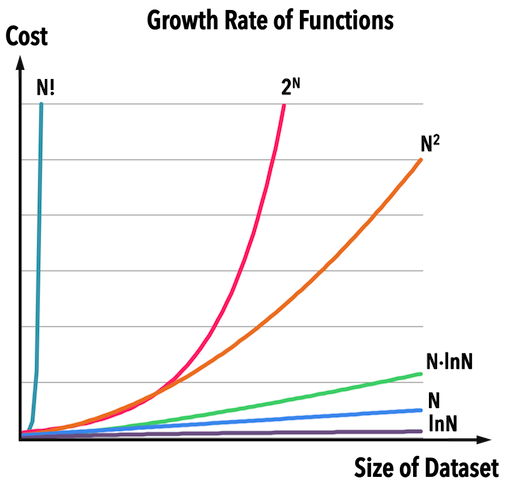
假設某間出版社想要印書，找到一間印刷廠，廠房內共有六台機器，每台機器的工作效率分別如圖一的六個函數，橫軸表示「書的數量」，縱軸表示「需要的工作天」。

	$N!$	$2^N$	$N^2$	$N\ln{N}$	$N$	$\ln{N}$
$N=5$	$120$	$32$	$25$	$8.05$	$5$	$1.6$
$N=100$	$9\times10^{157}$	$1.3\times10^{30}$	$10000$	$460$	$100$	$4.6$

表一

根據表一可以看出，若要印$N=5$本書：

使用「機器$\ln{N}$」需要$1.6$個工作天。
使用「機器$N^2$」需要$25$個工作天；
使用「機器$N!$」需要$120$個工作天；

當問題的資料量不大時，「有效率」的機器和「沒有效率」的機器在成本消耗上可能差異不大，但是當資料量增加時，成本會變得非常可觀。

若考慮印$N=100$本書：

使用「機器$\ln{N}$」需要$4.6$個工作天。
使用「機器$N^2$」需要$10000$個工作天，大約是$27$年；
使用「機器$N!$」需要$9\times10^{157}$個工作天，是個天文數字；

根據以上描述：

成本(包含運算時間與記憶體空間)，通常會和「待處理的資料量」有關，當資料量越大，成本會以某種關係(線性、指數等等，見圖一)跟著提高。
當資料量大時，演算法的效率很重要。

而圖一中，描述每一種演算法(一台機器代表一種演算法)的「工作效率之函數」，就稱為此演算法之Complexity(複雜度)。

使用Asymptotic Notation的優點

若能得知各個演算法的Complexity(複雜度)，便能決定哪個演算法較有效率。

但是並非所有演算法都像只有兩個迴圈的Insertion Sort那麼簡潔而容易分析，所以在評估演算法之Complexity(複雜度)時，常使用Asymptotic Notation(漸進符號)，其概念為：

希望能以「簡單的函數」(例如：$N^{2}、\ln{N}$等等)來描述Complexity(複雜度)的「趨勢」，特別是針對資料量非常大的時候。

以下分別介紹五個Asymptotic Notation(漸進符號)。

$\Theta-$Notation，Big-Theta

Asymptotic Notation(漸進符號)是所有能夠描述演算法趨勢的「函數之集合」，給定：

非負函數$f(n)$：描述演算法之趨勢。
非負函數$g(n)$：簡單函數。

若滿足以下定義：

$$ \Theta(g(n))=\{\,f(n)：存在正整數\:c_1,c_2,n_0 \,,並且對於所有n\geq n_0,\,滿足 0\leq c_{1}g(n)\leq f(n) \leq c_{2}g(n)\:\} $$

表示$g(n)$為$f(n)$趨勢之「邊界」(bound)，即可使用$g(n)$來描述$f(n)$之趨勢，以$f(n)\in\Theta(g(n))$表示(也會看到$f(n)=\Theta(g(n))$，但切記，$\Theta(g(n))$是一個集合)。

圖二：。

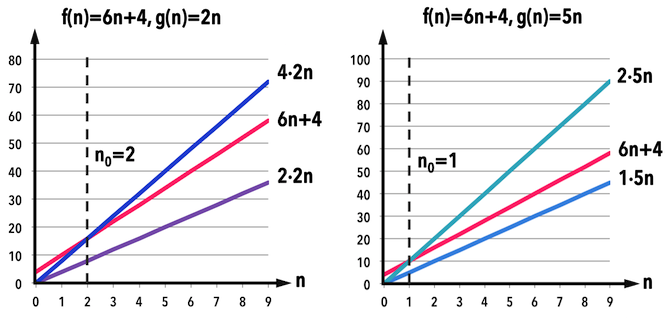
舉例來說，若現有一個演算法之趨勢可以用$f(n)=6n+4$代表，那麼以下兩個$g(n)$都能夠在$\Theta(g(n))$的定義下視為$f(n)$的「邊界」：

若$g(n)=2n$，取$c_{1}=2,c_{2}=4,n_{0}=2$，則滿足：
- $0\leq 2(2n)\leq 6n+4 \leq 4(2n) \,, \forall n\geq 2$，見圖二左。
  也就是說，當資料量$n\geq 2$，$f(n)=6n+4$的值往上不會超過$8n$，往下不會低於$4n$。
若$g(n)=5n$，取$c_{1}=1,c_{2}=2,n_{0}=1$，則滿足：
- $0\leq 1(5n)\leq 6n+4 \leq 2(5n) \,, \forall n\geq 1$，見圖二右。
  同理，當資料量$n\geq 1$，$f(n)=6n+4$的值往上不會超過$10n$，往下不會低於$5n$。

根據定義，既然係數($c_{1},c_{2}$)可以任選，那麼以上兩個$g(n)$函數其實可以把係數都提到$c_{1},c_{2}$裡，以同一個函數：$g(n)=n$表示即可。

由此可以確認，$\Theta(g(n))$是多個函數的「集合」。

若一個演算法之「趨勢」為$f(n)=6n+4$，那麼其複雜度即為$\Theta(n)$，可以表示成：

$f(n)\in\Theta(n)$，或者
$f(n)=\Theta(n)$。

以上情況可以推廣至所有的多項式(polynomial)，以$f(n)=3n^{3}+4n^{2}+5$為例，當$n$越來越大時，對$f(n)$之趨勢具有決定性影響力的是「最高次項」，此例為「三次方項」，所以，$f(n)$的複雜度為$\Theta(n^{3})$，將係數拿進$c_{1},c_{2}$，便以

$f(n)\in\Theta(n^{3})$，或者
$f(n)=\Theta(n^{3})$表示。

Big-Theta($\Theta(·)$)是同時找到$f(n)$的「上界(upper bound)」與「下界(lower bound)」，像是三明治一樣把$f(n)$夾住。

若把「上界」與「下界」分開來看，就是下面要介紹的Big-O與Big-Omega。

$O-$Notation，Big-O

一般談論的演算法之複雜度，經常是指Big-O，因為在估算成本時，最想知道的是「上界(upper bound)」，以第一小節的範例來說，就是要知道印$N$本書，每台機器「最久」要花多少時間。

Big-O定義如下：

$$ O(g(n))=\{\,f(n)：存在正整數\:c,n_0 \,,並且對於所有n\geq n_0,\,滿足 0\leq f(n) \leq cg(n)\:\} $$

根據定義，可以將Big-O視為Big-Theta($\Theta(·)$)的「上半部」，其以「簡單函數$g(n)$」描述$f(n)$在資料量夠大時，「最多」會達到怎麼樣的趨勢。

圖三：。

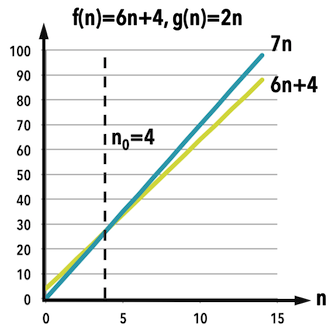
繼續以$f(n)=6n+4$為例，若選$g(n)=n,c=7,n_{0}=4$，即可滿足：

$0\leq 6n+4 \leq 7n \,, \forall n\geq 4$，見圖三。
表示$f(n)$之「上界」趨勢能夠以$g(n)=7n$描述。

同樣的，把係數放進正整數$c$裡面，$f(n)$之複雜度在Big-O的定義下，可以用簡單函數$g(n)=n$表示：

$f(n)\in O(n)$，或者
$f(n)=O(n)$。

再多看幾個例子：

若$f(n)=6n^{3}+5n^{2}-4n\log{n}+3$，那麼此函數之複雜度為$f(n)=O(n^{3})$。
若$f(n)=2$，此函數之複雜度為$f(n)=O(1)$，表示此演算法之效率「與資料量多寡無關」，又稱為常數時間(constant time)的複雜度。

$\Omega-$Notation，Big-Omega

若想知道某個演算法「至少」需要多少時間時，便可以Big-Omega來估算「下界(lower bound)」。

Big-Omega的定義如下：

$$ \Omega(g(n))=\{\,f(n)：存在正整數\:c,n_0 \,,並且對於所有n\geq n_0,\,滿足 0\leq cg(n) \leq f(n)\:\} $$

Big-Omega可以視為Big-Theta($\Theta(·)$)的「下半部」，其以「簡單函數$g(n)$」描述$f(n)$在資料量夠大時，「至少」會達到怎麼樣的趨勢。

繼續以$f(n)=6n+4$為例，$f(n)$之複雜度在Big-Omega的定義下，可以用簡單函數$g(n)=n$表示：

$f(n)\in \Omega(n)$，或者
$f(n)=\Omega(n)$。

以上介紹的Big-O($O(·)$)與Big-Omega($\Omega(·)$)是夾得「比較緊的(tight)」上界和下界，接下來還有兩個符號：Littel-o($o(·)$)與Littel-omega($\omega(·)$)，表示「沒有那麼緊的」上下界。

$o-$Notation，Littel-o

Littel-o($o(·)$)的定義如下：

$$ o(g(n))=\{\,f(n)：對於所有正整數\:c,存在正整數\:n_0\,,使得對於所有n\geq n_0,\, 0\leq f(n) \leq cg(n)\:\} $$

怎麼說Littel-o($o(·)$)比較「不緊」呢？因為定義中是「對於所有正整數$c$」，因此$f(n)=o(g(n))$務必要求$g(n)$的「成長率」遠遠大於$f(n)$，等同於滿足以下極限關係式：

$$ \lim_{n->\infty}\frac{f(n)}{g(n)}=0 $$

比較Big-O($O(·)$)與Littel-o($o(·)$)：

$2n=o(n^{2})$
$2n=O(n)$
$2n^{2}=o(n!)$
$2n^{2}=O(n^{2})$

$\omega-$Notation，Littel-omega

Littel-omega($\omega(·)$)的定義如下：

$$ \omega(g(n))=\{\,f(n)：對於所有正整數\:c,存在正整數\:n_0\,,使得對於所有n\geq n_0,\, 0\leq cg(n) \leq f(n)\:\} $$

同理，$f(n)=\omega(g(n))$要求$g(n)$的「成長率」遠遠小於$f(n)$，等同於滿足以下極限關係式：

$$ \lim_{n->\infty}\frac{f(n)}{g(n)}=\infty $$

比較Big-Omega($\Omega(·)$)與Littel-omega($\omega(·)$)：

$4n^{2}=\omega(n)$
$4n^{2}=\omega(\log{n})$
$4n^{2}=\Omega(n^{2})$

以上便是演算法之Complexity(複雜度)以及經常使用的Asymptotic Notation(漸進符號)之介紹。

最後再看一次常見的時間複雜度之效率比較：

圖一：。

根據圖一，若同樣處理$N$筆資料，那麼各個時間複雜度之成本如下：
(成本越高，表示效率越差)

$$ O(1)<O(\log{N})<O(N)<O(N\log{N})<O(N^{2})<O(2^{N})<O(N!) $$

最有效率的是常數的時間複雜度($O(1)$)，意思其「運算成本與資料量無關」，所以不管資料量多大，保證能夠在「可數(countable)、有限(finite)」的時間內完成，例如：

不管矩陣大小(size)有多大，一定能夠利用index在$O(1)$時間，對矩陣的元素做存取，例如Array[index]=5。
不管Linked list長度有多長，一定能夠在$O(1)$時間，在list的front指標後新增節點(insert node at the front)，參考：Linked List: 新增資料、刪除資料、反轉。

各個常見演算法的時間複雜度(Big-O)可以參考：

Big-O Algorithm Complexity Cheat Sheet

參考資料：

Complexity系列文章

Complexity：Asymptotic Notation(漸進符號)

回到目錄：

目錄：演算法與資料結構

	\(N!\)	\(2^N\)	\(N^2\)	\(N\ln{N}\)	\(N\)	\(\ln{N}\)
\(N=5\)	\(120\)	\(32\)	\(25\)	\(8.05\)	\(5\)	\(1.6\)
\(N=100\)	\(9\times10^{157}\)	\(1.3\times10^{30}\)	\(10000\)	\(460\)	\(100\)	\(4.6\)

Complexity：Asymptotic Notation(漸進符號)

先備知識與注意事項

目錄

Complexity(複雜度)

使用Asymptotic Notation的優點

\(\Theta-\)Notation，Big-Theta

\(O-\)Notation，Big-O

\(\Omega-\)Notation，Big-Omega

\(o-\)Notation，Littel-o

\(\omega-\)Notation，Littel-omega

參考資料：

Complexity系列文章