Stack: 能夠在O(1)取得最小值的MinStack

先備知識與注意事項

眾所皆知，若手上處理的資料結構是Stack，除了「最上面」的資料可以輕易讀取(利用top())，若要知道Stack中的其餘資料，就只能透過從Stack的最上方把資料一個一個pop()後，才能檢視，時間複雜度為O(\(N\))。

如果想要在O(\(1\))的時間複雜度取得Stack中的「最小值」資料，該如何設計呢？

圖一。

以圖一為例，因為圖一是Stack的剖面圖，所以很容易可以看出，目前Stack中的最小值為\(4\)。但是一般的Stack並沒有提供剖面圖這種東西，只能透過函式top()來得知Stack「最上面」的\(9\)。

本篇文章要介紹的便是能夠在O(\(1\))的時間複雜度，得知目前Stack裡的「最小值」的進化版Stack，以下稱為MinStack。

在程式範例中將使用標準模板函式庫(STL)的std::stack<int>，其基本函式功能可以參考Stack: Intro(簡介)，更多內容請參考：Cplusplus：std::stack。

以兩個Stack來實作MinStack

要實作出MinStack的關鍵就是在一個class MinStack中使用「兩個Stack」，其中一個Stack用來存放資料(稱為datastack)，另一個用來記錄「目前最小值」(稱為minstack)。

在Push()新增資料時：

datastack一如往常以push()將資料放進Stack中。
minstack就必須判斷「欲新增的資料」是否有比「目前最上面」還要小。
- 如果有，就把「欲新增的資料」push()進minstack，此時該資料會位在Stack的「最上面」。
  - 特例：如果原先minstack裏面沒有資料，那麼就直接將「欲新增的資料」push()進minstack。
  - 透過這個步驟，可以保證minstack的「最上面」資料就是datastack中的「最小值」。
- 如果沒有，就把minstack「目前最上面」的資料，再push()進minstack一次，表示在新增資料後，「最小值」不變。

以圖二(a)為例，先後進行了「新增\(6\)」與「新增\(13\)」：

在新增\(6\)時：
- 以push(6)將\(6\)放進datastack。
- 因為minstack目前是空的，便同樣以push(6)將\(6\)放進minstack。
- 從minstack的「最上面」資料可以得知，目前datastack中的「最小值」是\(6\)。
在新增\(13\)時：
- 以push(13)將\(13\)放進datastack。
- 判斷出\(13\)與目前minstack的「最上面」資料何者較小，並將較小者push()進minstack。
- 同樣地，透過minsatck的「最上面」資料，可以得知目前datastack中的「最小值」仍然是\(6\)。

圖二(a)。

接著又新增了\(4\)、\(9\)、\(1\)，觀察圖二(b)，minstack的「最上面」資料，一定記錄著datastack的「最小值」。

圖二(b)。

由於Push()新增資料時對minstack的處理，在Pop()刪除資料時，datastack和minstack只要同步進行pop()即可，觀察圖三，每一次之後，minstack的「最上面」資料仍然是datastack的「最小值」。

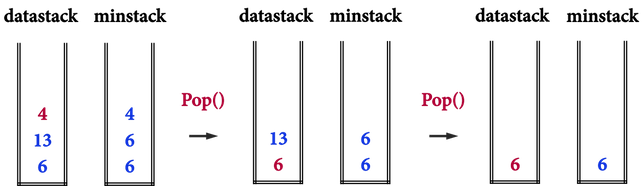
圖三。

程式碼

完整程式範例如下：

// C++ code
#include <iostream>
#include <stack>        // std::stack<>

class MinStack{
private:
    std::stack<int> data;
    std::stack<int> minstack;
public:
    MinStack(){};
    void Push(int x);
    void Pop();
    bool IsEmpty();
    int Top();
    int getSize();
    int getMin();
};
void MinStack::Push(int x){

    data.push(x);
    if (minstack.empty() || x < minstack.top()) {
        minstack.push(x);
    }
    else {
        minstack.push(minstack.top());
    }
}

void MinStack::Pop(){

    if (data.empty()) {
        std::cout << "Stack is empty.\n";
        return;
    }
    data.pop();
    minstack.pop();
}

int MinStack::getMin(){

    if (data.empty()) {
        std::cout << "Stack is empty.\n";
        return -1;
    }

    return minstack.top();
}

bool MinStack::IsEmpty(){

    return data.empty();
}

int MinStack::Top(){

    if (data.empty()) {
        std::cout << "Stack is empty.\n";   // sorry for the bad exception handling
        return -1;                          
    }

    return data.top();
}

int MinStack::getSize(){

    if (data.empty()) {
        std::cout << "Stack is empty.\n";
        return -1;
    }

    return (int)data.size();
}

int main(){

    MinStack s;
    s.Pop();
    s.Push(6);
    std::cout << "\ntop: " << s.Top() << "\nmin: " << s.getMin() << std::endl;

    s.Push(13);
    std::cout << "\ntop: " << s.Top() << "\nmin: " << s.getMin() << std::endl;

    s.Push(4);
    std::cout << "\ntop: " << s.Top() << "\nmin: " << s.getMin() << std::endl;

    s.Push(9);
    std::cout << "\ntop: " << s.Top() << "\nmin: " << s.getMin() << std::endl;

    s.Push(1);
    std::cout << "\ntop: " << s.Top() << "\nmin: " << s.getMin() << std::endl;

    s.Pop();
    std::cout << "\ntop: " << s.Top() << "\nmin: " << s.getMin() << std::endl;

    s.Pop();
    std::cout << "\ntop: " << s.Top() << "\nmin: " << s.getMin() << std::endl;

    s.Pop();
    std::cout << "\ntop: " << s.Top() << "\nmin: " << s.getMin() << std::endl;

    s.Pop();
    std::cout << "\ntop: " << s.Top() << "\nmin: " << s.getMin() << std::endl;

    s.Pop();
    std::cout << "\ntop: " << s.Top() << "\nmin: " << s.getMin() << std::endl;

    return 0;
}

output:

Stack is empty.

top: 6
min: 6

top: 13
min: 6

top: 4
min: 4

top: 9
min: 4

top: 1
min: 1

top: 9
min: 4

top: 4
min: 4

top: 13
min: 6

top: 6
min: 6

top: Stack is empty.
-1
min: Stack is empty.
-1

以上便是分別以兩個std::stack<>實作MinStack的方法。

更多相關的討論，包括更節省記憶體空間的做法，請參考：Stack Overflow：design a stack such that getMinimum( ) should be O(1)。

參考資料：

Stack系列文章

Stack: Intro(簡介)
Stack: 以Array與Linked list實作
 Stack: 能夠在O(1)取得最小值的MinStack

回到目錄：

目錄：演算法與資料結構